
When a system such as an electron device is driven far from equilibrium by the application of an external voltage, both coherent and incoherent processes will generally occur within the device. Coherent processes include tunneling and ballistic transport, and incoherent processes include dissipative scattering via phonons, for example. Coherent effects are described by adding complex-valued amplitudes (that is, values of the wavefunction), which is done implicitly in the solution of Schrödinger 's equation above. Incoherent effects are described by superposition of real-valued probabilities. An example of such incoherent superposition is the summation of the current density over energies and transverse modes to obtain the total current density, as discussed in Subsection 2. We can formalize the statistical summation procedure described there into a mathematical object known as the density matrix [30,31]. In terms of the continuum position variable x, the density matrix is actually a complex-valued function of two arguments, and has the general form:
where the 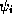 form a complete set of states ( not necessarily the eigenstates
of the Hamiltonian), and the
form a complete set of states ( not necessarily the eigenstates
of the Hamiltonian), and the 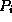 are real-valued probabilities for finding an electron
in each state
are real-valued probabilities for finding an electron
in each state 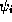 . With this definition, the expectation value of any physical
observable represented by an operator A is given by:
. With this definition, the expectation value of any physical
observable represented by an operator A is given by:
where A is taken to operate with respect to the first argument of 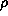 . Inserting
(73) into (74) and rearranging the expression, we get the
more familiar form for the expectation value:
. Inserting
(73) into (74) and rearranging the expression, we get the
more familiar form for the expectation value:
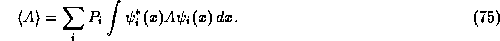
In particular, the particle density is given by

and the current density is

If 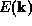 is non-parabolic, a more complicated expression is required for
the current density.
is non-parabolic, a more complicated expression is required for
the current density.
If the motion of the particles described by the density matrix is purely ballistic (no energy loss) and defined by a Hamiltonian H, the equation describing the evolution of the density matrix may be derived by substituting Schrödinger 's equation into (73). The result is the Liouville-von Neumann equation:
where 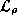 is a linear operator which operates upon the density matrix and is
called the Liouville operator. (Since it operates upon
is a linear operator which operates upon the density matrix and is
called the Liouville operator. (Since it operates upon 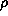 , which is
itself a quantum-mechanical operator,
, which is
itself a quantum-mechanical operator, 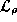 is technically a superoperator
[5].) The Liouville equation acts upon the density matrix by
evolving the wavefunctions, but does not change the probabilities
is technically a superoperator
[5].) The Liouville equation acts upon the density matrix by
evolving the wavefunctions, but does not change the probabilities 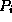 . This is
a characteristic of ballistic, or conservative, motion. Irreversible, or dissipative,
processes involve transitions between quantum states, and are described by operators
which modify the probabilities
. This is
a characteristic of ballistic, or conservative, motion. Irreversible, or dissipative,
processes involve transitions between quantum states, and are described by operators
which modify the probabilities 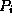 . Such operators are discussed below.
. Such operators are discussed below.
In the classical systems, the quantity which describes the state of the system
corresponding to 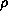 is the phase-space distribution function
is the phase-space distribution function 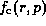 where
r is now the position and p is the momentum. The classical Liouville equation is
where
r is now the position and p is the momentum. The classical Liouville equation is
where v is the velocity and V is the potential in which the particles are moving. The particle and current densities are obtainable from the classical distribution function by
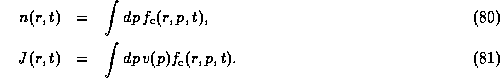
The Liouville equation, in either the classical (79) or quantum
(78) context, describes only ideal, conservative motion. Within the
scope of these equations, particles can only oscillate within the system, unless one
applies boundary conditions which permit particles to escape from
it. The form of the equations (for closed systems)
does not describe an approach to a steady-state, neither
equilibrium nor non-equilibrium. The reason for this involves the eigenvalue spectrum
of  and
and  . The solutions of (78) will consist of a linear
combination of terms with time dependence
. The solutions of (78) will consist of a linear
combination of terms with time dependence 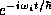 , where
, where
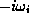 are the eigenvalues of
are the eigenvalues of 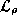 .
The Liouville operator [as defined in (78), including the imaginary
factor] is anti-Hermitian, so the frequencies
.
The Liouville operator [as defined in (78), including the imaginary
factor] is anti-Hermitian, so the frequencies 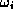 are purely real.
Thus the transformation which maps the state of the system at some initial time into
some later time is a unitary linear transformation, and we will call the behavior
described by such equations ``unitary time evolution.''
Devices of course usually approach a steady state after
a sufficiently long time. To describe this behavior, we must incorporate irreversible
processes into the equations.
are purely real.
Thus the transformation which maps the state of the system at some initial time into
some later time is a unitary linear transformation, and we will call the behavior
described by such equations ``unitary time evolution.''
Devices of course usually approach a steady state after
a sufficiently long time. To describe this behavior, we must incorporate irreversible
processes into the equations.