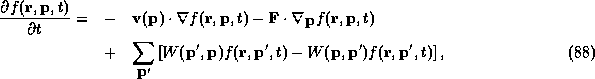
The Boltzmann equation is the basis for the standard models of electron transport in semiconductors in a semi-classical approximation. It consists of the classical Liouville equation (79) augmented by a master operator of precisely the form (84) to describe collisions between electrons and other particles. The Boltzmann equation is commonly written in the form [35]:
where 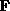 is the force on the electron (due to the electric field, for example).
is the force on the electron (due to the electric field, for example).
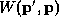 is the scattering rate from
is the scattering rate from 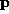 to
to  , as
in (82), but now
, as
in (82), but now  is a continuous variable.
These scattering rates are conventionally obtained by evaluating the Fermi golden
rule for scattering between plane-wave states with wavevectors
is a continuous variable.
These scattering rates are conventionally obtained by evaluating the Fermi golden
rule for scattering between plane-wave states with wavevectors
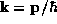 , and
, and 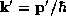 . Note that
these are the scattering rates between infinitely extended states, but in the
Boltzmann equation, each scattering event is assumed to take place at a
single point. (If we did not assume this, the continuity equation would be violated.)
. Note that
these are the scattering rates between infinitely extended states, but in the
Boltzmann equation, each scattering event is assumed to take place at a
single point. (If we did not assume this, the continuity equation would be violated.)
The different scattering mechanisms in semiconductors and their rates has been the subject of much theoretical and experimental work. Expressions for these scattering rates can be found in the works of Conwell [36], and Ridley [37]. The evaluation of low-field transport properties of bulk semiconductors is described in detail by Rode [38]