



Next: The Wigner Distribution
Up: Irreversible Processes and
Previous: The Boltzmann Equation
The solution of the Boltzmann equation presents a rather difficult problem, because
of the large number of variables involved. For a general three-dimensional system
there are six arguments of the distribution function (three components each of  and
and 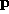 ). If we were to simply discretize the Boltzmann equation, we would
need to represent the distribution function f by an array with six subscripts,
corresponding to the six arguments of the continuous function. If we used only
ten values for each subscript, the f array would have
). If we were to simply discretize the Boltzmann equation, we would
need to represent the distribution function f by an array with six subscripts,
corresponding to the six arguments of the continuous function. If we used only
ten values for each subscript, the f array would have 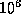 elements, and each
evaluation of f would require a corresponding number of operations. Such a
discretization of the Boltzmann equation has in fact been investigated by Aubert,
Vaissiere, and Nougier [39], for the case of a spatially homogeneous
system, so that only the three velocity arguments are required.
elements, and each
evaluation of f would require a corresponding number of operations. Such a
discretization of the Boltzmann equation has in fact been investigated by Aubert,
Vaissiere, and Nougier [39], for the case of a spatially homogeneous
system, so that only the three velocity arguments are required.
By far the most widely used technique for evaluating the Boltzmann description
of electron transport has been the Monte Carlo method [40,41,42,43].
With this technique, one does not solve the Boltzmann equation directly, but
one rather simulates the motion of classical electrons subjected to a combination
of free-flight motion and instantaneous random scattering events. The
distribution function is then estimated by statistical averages over long times
or many particles. The state of the system is represented by the position and
velocity vectors of each of a large number of particles. The velocity and position
of each particle are integrated over time until a collision is deemed to have
occurred (based upon the
value of a randomly-chosen value with an appropriate distribution). Other random
values then determine the particular scattering mechanism and the velocity of the
electron after the scattering. After the scattering, the free-flight motion of the
electron is again integrated until the next collision. This procedure is performed
for all particles in the chosen ensemble to evaluate the time-evolution of the
device. The openness of the device is modeled by procedures which treat the
escape of electrons into and injection of electrons from the contact regions
[44,45].
The Monte Carlo technique permits one to include many of the physical effects
that influence electron transport, and to include them at an extremely detailed
level. Effects which have been incorporated include the detailed energy-band
structure of the semiconductor [46], electron-electron interactions
at the level of
the self-consistent potential or at a more detailed electron-electron collision
description [47], and higher-energy events such as impact
ionization [45]. However, there is one very significant constraint imposed
by the Monte Carlo procedure: only processes describable by a master operator
can be modeled.




Next: The Wigner Distribution
Up: Irreversible Processes and
Previous: The Boltzmann Equation
William R. Frensley
Fri Jun 23 15:00:21 CDT 1995
 and
and 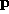 ). If we were to simply discretize the Boltzmann equation, we would
need to represent the distribution function f by an array with six subscripts,
corresponding to the six arguments of the continuous function. If we used only
ten values for each subscript, the f array would have
). If we were to simply discretize the Boltzmann equation, we would
need to represent the distribution function f by an array with six subscripts,
corresponding to the six arguments of the continuous function. If we used only
ten values for each subscript, the f array would have 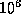 elements, and each
evaluation of f would require a corresponding number of operations. Such a
discretization of the Boltzmann equation has in fact been investigated by Aubert,
Vaissiere, and Nougier [39], for the case of a spatially homogeneous
system, so that only the three velocity arguments are required.
elements, and each
evaluation of f would require a corresponding number of operations. Such a
discretization of the Boltzmann equation has in fact been investigated by Aubert,
Vaissiere, and Nougier [39], for the case of a spatially homogeneous
system, so that only the three velocity arguments are required.