



Next: Green's Functions
Up: Irreversible Processes and
Previous: Numerical Evaluation Methods
The Wigner distribution function is a mathematical transform of the density matrix
which approaches the classical distribution function 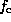 as the system becomes
classical (with large dimensions, slowly varying potentials, and/or high temperatures)
[5,48,49,50,51]. This representation of
the statistical state has proven to be useful in modeling quantum-effect devices
such as the resonant-tunneling diode [52,53,54,55].
as the system becomes
classical (with large dimensions, slowly varying potentials, and/or high temperatures)
[5,48,49,50,51]. This representation of
the statistical state has proven to be useful in modeling quantum-effect devices
such as the resonant-tunneling diode [52,53,54,55].
To derive the Wigner
function from the density matrix 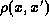 defined in (73)
one rewrites the arguments
defined in (73)
one rewrites the arguments
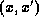 as
as 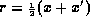 and
and 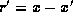 , and then Fourier transforms
, and then Fourier transforms
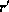 into a momentum variable p. Thus:
into a momentum variable p. Thus:
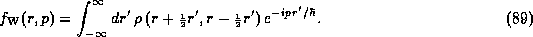
Applying the same procedure (which is known as the Wigner-Weyl transformation) to
the Liouville-von Neumann equation (78) gives:
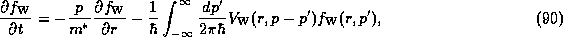
where the kernel of the potential operator is given by:
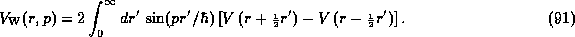
Let us examine the form of these equations. Because (90) is
derived from (78) by a mathematical transformation, we would expect
that it should also describe unitary time evolution. The condition for unitary
evolution is that 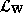 be an anti-Hermitian operator. The potential operator
is anti-Hermitian [because
be an anti-Hermitian operator. The potential operator
is anti-Hermitian [because 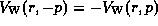 ], and the drift term is anti-Hermitian
if periodic boundary conditions are imposed. On the other hand, we have seen that
if initial conditions are imposed, the drift term is a master operator, and the
equation then describes irreversible time evolution. This is the origin of the usefulness
of the Wigner representation for describing electron devices. One applies boundary
conditions to
], and the drift term is anti-Hermitian
if periodic boundary conditions are imposed. On the other hand, we have seen that
if initial conditions are imposed, the drift term is a master operator, and the
equation then describes irreversible time evolution. This is the origin of the usefulness
of the Wigner representation for describing electron devices. One applies boundary
conditions to 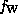 so as to fix the distribution of electrons entering the domain:
so as to fix the distribution of electrons entering the domain:

where 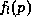 and
and 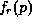 are the distribution functions in the left- and right-hand
contacts (reservoirs), respectively. Because these boundary conditions introduce
irreversibility into the Liouville equation, one can now evaluate the time-evolution
of a device, and observe an approach to steady-state [5].
Inelastic processes such as phonon scattering may be included in a semi-classical
way by adding the Boltzmann collision term [the integral expression in (88)]
to the Liouville equation (78) [56,54],
or by even simpler schemes such as the relaxation time approximation
[53,57].
are the distribution functions in the left- and right-hand
contacts (reservoirs), respectively. Because these boundary conditions introduce
irreversibility into the Liouville equation, one can now evaluate the time-evolution
of a device, and observe an approach to steady-state [5].
Inelastic processes such as phonon scattering may be included in a semi-classical
way by adding the Boltzmann collision term [the integral expression in (88)]
to the Liouville equation (78) [56,54],
or by even simpler schemes such as the relaxation time approximation
[53,57].
The open-system Wigner function approach has proved to be of use in understanding
the behavior of resonant-tunneling diodes. This technique permits evaluation of
steady-state behavior in the form of the 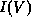 curve, and calculations of the large-signal
transient response and small-signal ac response [5]. The
curve, and calculations of the large-signal
transient response and small-signal ac response [5]. The 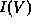 curves derived from this model show the expected negative differential-conductance
region, but the ratio of the peak to valley currents is always smaller than that
obtained from the tunneling theory (38), and is often less than
that observed experimentally. Recently,
Tsuchiya and co-workers have developed an improved formulation of the Liouville equation
(90) which takes the spatial variation of the effective mass into
account, and which
leads to larger peak-to-valley ratios than the simpler theory [58].
These different
formulations are compared in Figure 2.
curves derived from this model show the expected negative differential-conductance
region, but the ratio of the peak to valley currents is always smaller than that
obtained from the tunneling theory (38), and is often less than
that observed experimentally. Recently,
Tsuchiya and co-workers have developed an improved formulation of the Liouville equation
(90) which takes the spatial variation of the effective mass into
account, and which
leads to larger peak-to-valley ratios than the simpler theory [58].
These different
formulations are compared in Figure 2.
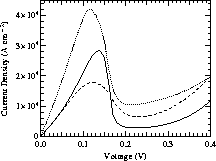
Figure 2: Theoretical  curves for a model resonant-tunneling diode structure
. The solid line shows the results of the tunneling theory, equation
(28). The dashed line shows the result of evaluating the Wigner
function using a local model of the variation of the effective mass [52].
The dotted line shows the result of a Wigner function calculation using the nonlocal
effective-mass model of Tsuchiya and co-workers [58]. (Calculations by
C. Fernando, University of Texas at Dallas.)
curves for a model resonant-tunneling diode structure
. The solid line shows the results of the tunneling theory, equation
(28). The dashed line shows the result of evaluating the Wigner
function using a local model of the variation of the effective mass [52].
The dotted line shows the result of a Wigner function calculation using the nonlocal
effective-mass model of Tsuchiya and co-workers [58]. (Calculations by
C. Fernando, University of Texas at Dallas.)




Next: Green's Functions
Up: Irreversible Processes and
Previous: Numerical Evaluation Methods
William R. Frensley
Fri Jun 23 15:00:21 CDT 1995
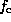 as the system becomes
classical (with large dimensions, slowly varying potentials, and/or high temperatures)
[5,48,49,50,51]. This representation of
the statistical state has proven to be useful in modeling quantum-effect devices
such as the resonant-tunneling diode [52,53,54,55].
as the system becomes
classical (with large dimensions, slowly varying potentials, and/or high temperatures)
[5,48,49,50,51]. This representation of
the statistical state has proven to be useful in modeling quantum-effect devices
such as the resonant-tunneling diode [52,53,54,55].
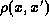 defined in (
defined in (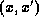 as
as 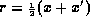 and
and 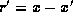 , and then Fourier transforms
, and then Fourier transforms
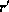 into a momentum variable p. Thus:
into a momentum variable p. Thus:
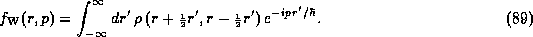
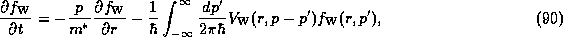
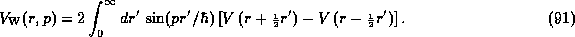
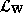 be an anti-Hermitian operator. The potential operator
is anti-Hermitian [because
be an anti-Hermitian operator. The potential operator
is anti-Hermitian [because 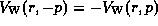 ], and the drift term is anti-Hermitian
if periodic boundary conditions are imposed. On the other hand, we have seen that
if initial conditions are imposed, the drift term is a master operator, and the
equation then describes irreversible time evolution. This is the origin of the usefulness
of the Wigner representation for describing electron devices. One applies boundary
conditions to
], and the drift term is anti-Hermitian
if periodic boundary conditions are imposed. On the other hand, we have seen that
if initial conditions are imposed, the drift term is a master operator, and the
equation then describes irreversible time evolution. This is the origin of the usefulness
of the Wigner representation for describing electron devices. One applies boundary
conditions to 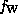 so as to fix the distribution of electrons entering the domain:
so as to fix the distribution of electrons entering the domain:

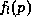 and
and 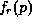 are the distribution functions in the left- and right-hand
contacts (reservoirs), respectively. Because these boundary conditions introduce
irreversibility into the Liouville equation, one can now evaluate the time-evolution
of a device, and observe an approach to steady-state [
are the distribution functions in the left- and right-hand
contacts (reservoirs), respectively. Because these boundary conditions introduce
irreversibility into the Liouville equation, one can now evaluate the time-evolution
of a device, and observe an approach to steady-state [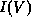 curve, and calculations of the large-signal
transient response and small-signal ac response [
curve, and calculations of the large-signal
transient response and small-signal ac response [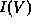 curves derived from this model show the expected negative differential-conductance
region, but the ratio of the peak to valley currents is always smaller than that
obtained from the tunneling theory (
curves derived from this model show the expected negative differential-conductance
region, but the ratio of the peak to valley currents is always smaller than that
obtained from the tunneling theory (
 curves for a model resonant-tunneling diode structure
. The solid line shows the results of the tunneling theory, equation
(28). The dashed line shows the result of evaluating the Wigner
function using a local model of the variation of the effective mass [52].
The dotted line shows the result of a Wigner function calculation using the nonlocal
effective-mass model of Tsuchiya and co-workers [58]. (Calculations by
C. Fernando, University of Texas at Dallas.)
curves for a model resonant-tunneling diode structure
. The solid line shows the results of the tunneling theory, equation
(28). The dashed line shows the result of evaluating the Wigner
function using a local model of the variation of the effective mass [52].
The dotted line shows the result of a Wigner function calculation using the nonlocal
effective-mass model of Tsuchiya and co-workers [58]. (Calculations by
C. Fernando, University of Texas at Dallas.)