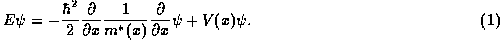
Let us consider a one-dimensional, single-band model. In a semiconductor heterostructure, the electron wavefunctions are described most simply by the effective-mass Schrödinger equation:
The form of the kinetic-energy operator in (1) is the simplest
Hermitian form one can use if the materials parameters (such as the effective
mass 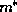 ) vary with position [7,8]. Now, let us assume that
all variation of the potential and of the materials parameters are confined
to an interval
) vary with position [7,8]. Now, let us assume that
all variation of the potential and of the materials parameters are confined
to an interval 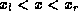 , so that outside of this interval the form of
Schrödinger 's equation is translationally invariant. Thus, in the regions
, so that outside of this interval the form of
Schrödinger 's equation is translationally invariant. Thus, in the regions 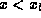 and
and 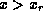 (the ``asymptotic regions''), the solutions of Schrödinger 's equation
are superpositions of plane waves, and the energies of these plane waves are
described by a well-defined dispersion relation
(the ``asymptotic regions''), the solutions of Schrödinger 's equation
are superpositions of plane waves, and the energies of these plane waves are
described by a well-defined dispersion relation 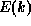 . We will refer to
quantities in the asymptotic regions by the subscripts l and r for the
left- and right-hand regions, respectively.
. We will refer to
quantities in the asymptotic regions by the subscripts l and r for the
left- and right-hand regions, respectively.
Now, for any energy  and
and 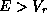 , there will be two independent
solutions to Schrödinger 's equation representing electrons incident from the
left and the right, respectively. In the asymptotic regions, these
solutions will have the form:
, there will be two independent
solutions to Schrödinger 's equation representing electrons incident from the
left and the right, respectively. In the asymptotic regions, these
solutions will have the form:
In general, 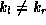 because
because 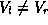 . There exist several
rigorous relationships between the transmission and reflection amplitudes
. There exist several
rigorous relationships between the transmission and reflection amplitudes
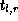 and
and 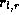 . Invoking Green's identity leads to the
current-continuity equations
. Invoking Green's identity leads to the
current-continuity equations
and an orthogonality condition
One may also invoke time-reversal symmetry to find the relationship between
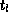 and
and 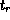 . Noting that
. Noting that 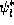 , say, is a solution of
Schrödinger 's equation with energy E, it must be possible to write
, say, is a solution of
Schrödinger 's equation with energy E, it must be possible to write 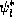 as a linear combination of
as a linear combination of 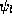 and
and 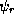 . With a bit of manipulation,
one finds
. With a bit of manipulation,
one finds
In most textbooks, the relations (1--7) are presented with the
wavenumbers 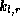 in place of the velocities
in place of the velocities 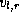 . Such expressions
are derived within the assumptions that the dispersion relation (or band structure)
. Such expressions
are derived within the assumptions that the dispersion relation (or band structure) 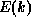 is perfectly parabolic and does not depend upon position. Neither assumption is
warranted in semiconductor heterostructures, as electrons in heterostructure devices
frequently explore non-parabolic regions of the energy-band structure, and the
band structure itself (particularly the effective mass) will vary with semiconductor
composition and thus position. The expressions (1--7)
are valid for nonparabolic and spatially varying
dispersion relations and should thus always be used. The velocity is the electron
group velocity, given by
is perfectly parabolic and does not depend upon position. Neither assumption is
warranted in semiconductor heterostructures, as electrons in heterostructure devices
frequently explore non-parabolic regions of the energy-band structure, and the
band structure itself (particularly the effective mass) will vary with semiconductor
composition and thus position. The expressions (1--7)
are valid for nonparabolic and spatially varying
dispersion relations and should thus always be used. The velocity is the electron
group velocity, given by
using the dispersion relation appropriate to the given semiconductor material.
One conventionally defines the transmission probability T as the ratio of the transmitted to the incident flux, or

so that T is same for both directions of incidence. One can also show, using equations (1--7),

(Because the reflection probability is measured on the same side of the system as the incident flux, there is no velocity correction.) Also note that, from (1),

as one would expect.
Finally, we investigate the normalization and orthogonality properties
of the scattering states. Because we are dealing with a continuum of
states over which we must integrate to evaluate any physical observable,
a ``delta-function'' normalization is appropriate. With such a normalization
convention, any finite contribution to the inner product, such as the
integral over 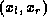 , may be neglected in comparison to the integrals
over
, may be neglected in comparison to the integrals
over 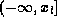 and
and  . Thus,
. Thus,
A relationship similar to (12) can be written for
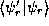 . The
. The 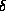 -functions can be rewritten
in terms of the energy E using
-functions can be rewritten
in terms of the energy E using
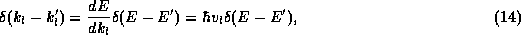
and similarly for  . We then obtain
. We then obtain
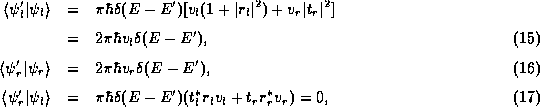
from equations (1).