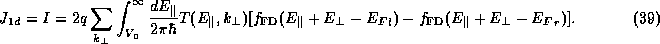Next: Evaluation of Scattering-State
Up: Tunneling Theory
Previous: General Formulation
To evaluate any physical observables, such as the current density, we must
specify how the scattering solutions are statistically weighted in the final
result. For the case of a continuous spectrum of states, with 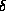 -function
normalization, the derivation of the correct expressions are rather tricky, because
we seek expressions for densities of charge, current, energy, etc., rather than total
quantities (which are of course infinite in an unbounded system). To illustrate
the procedure, let us follow through the derivation of the electron density in
a spatially uniform three-dimensional semiconductor in equilibrium. We approximate
the conduction band structure by a simple parabolic dispersion relation:
-function
normalization, the derivation of the correct expressions are rather tricky, because
we seek expressions for densities of charge, current, energy, etc., rather than total
quantities (which are of course infinite in an unbounded system). To illustrate
the procedure, let us follow through the derivation of the electron density in
a spatially uniform three-dimensional semiconductor in equilibrium. We approximate
the conduction band structure by a simple parabolic dispersion relation:

where 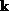 is the wavevector. The probability that each state
is the wavevector. The probability that each state 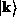 will be occupied by an electron is given by the Fermi-Dirac distribution function:
will be occupied by an electron is given by the Fermi-Dirac distribution function:
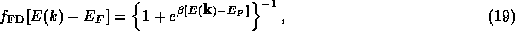
where 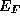 is the Fermi level or chemical potential and
is the Fermi level or chemical potential and 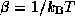 , T
being the absolute temperature. (To avoid confusion with the transmission probability
which is also denoted by T, the absolute temperature will always be shown
multiplied by Boltzmann's constant
, T
being the absolute temperature. (To avoid confusion with the transmission probability
which is also denoted by T, the absolute temperature will always be shown
multiplied by Boltzmann's constant  .)
Let us now
make an ad hoc assumption that the semiconductor crystal is a cube with each
side of length L, and
apply periodic boundary conditions. Then the stationary quantum states are plane
waves (normalized to unit amplitude) of the form
.)
Let us now
make an ad hoc assumption that the semiconductor crystal is a cube with each
side of length L, and
apply periodic boundary conditions. Then the stationary quantum states are plane
waves (normalized to unit amplitude) of the form

Due to the periodic boundary conditions,  must assume discrete values:
must assume discrete values:
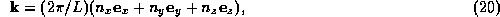
where 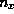 ,
, 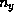 , and
, and 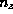 are integers. The total number of electrons in the
crystal N is just the sum over all of the states
are integers. The total number of electrons in the
crystal N is just the sum over all of the states 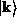 of the probability
that each state is occupied
of the probability
that each state is occupied

where the factor of 2 comes from the two spin states. Now, because L is large,
the allowed values
of 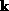 are very closely spaced, and the sum over
are very closely spaced, and the sum over 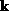 can be well
approximated by an integral:
can be well
approximated by an integral:

We can now write an expression for the density of electrons n:
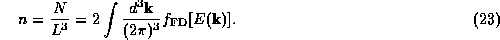
Notice that the arbitrary crystal dimension L has dropped out of the final expression.
In order to evaluate densities using expressions such as (23)
it is usually more convenient to transform the integration variable to E. By expressing
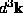 in spherical coordinates and
manipulating the dispersion relation (18) one finds [9]:
in spherical coordinates and
manipulating the dispersion relation (18) one finds [9]:
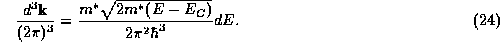
We will also have occasion to use the corresponding expressions for integrals over
two- and one-dimensional 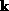 vectors. For the two-dimensional case (still
assuming a parabolic dispersion relation):
vectors. For the two-dimensional case (still
assuming a parabolic dispersion relation):

For integration over a one-dimensional k, the definition of the group velocity
(8) may be used to obtain an expression valid for any dispersion relation:

Inserting (24) into (23) leads to the usual expression
for the electron density in a semiconductor (as discussed in Chapter 1 of the present
volume) 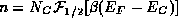 .
.
The procedure for evaluating a physical observable in an equilibrium system of infinite
extent may thus be generalized from the above discussion. The expectation
value of the observable quantity is calculated for each state, taking the scattering
states to be normalized to unit amplitude. The density of the observable is then
determined by inserting this expectation value into the sum in (23)
and evaluating the resulting integral, usually using the relations (2).
The two most important observables are the electron density 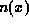 and the current
density j (which is independent of position in one dimension and steady-state).
The expectation value of the density for a state
and the current
density j (which is independent of position in one dimension and steady-state).
The expectation value of the density for a state 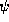 is simply
is simply

The expectation value of j is simple, though the operator itself often is not.
(Link to manuscript with full details.)
If the
dispersion relation 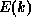 is not parabolic and independent of position, the form
of the operator j is not given by the simple textbook expression
is not parabolic and independent of position, the form
of the operator j is not given by the simple textbook expression
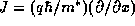 . The current density operator is
instead whatever remains of the kinetic energy term of the Hamiltonian after
the application of Green's identity as in the derivation of (1),
and this obviously depends upon the form of the Hamiltonian itself.
For unit-incident-amplitude scattering states, however, the result is invariably
. The current density operator is
instead whatever remains of the kinetic energy term of the Hamiltonian after
the application of Green's identity as in the derivation of (1),
and this obviously depends upon the form of the Hamiltonian itself.
For unit-incident-amplitude scattering states, however, the result is invariably
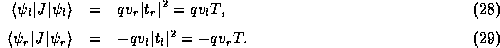
Of course, in equilibrium, these two currents cancel each other (by the
principle of detailed balance) and there is no net current flow.
To investigate the transport properties of a quantum system one must generally
evaluate the current flow through the system, and this requires that one examine
systems that are out of thermal equilibrium. A common situation, in both experimental
apparatus and technological systems, is that one has two (or more) physically large
regions densely populated with electrons in which the current density is low, coupled
by a smaller region through which the current density is much larger. It is
convenient to regard the large regions as ``electron reservoirs'' within which
the electrons are all in equilibrium with a constant temperature and Fermi level, and
which are so large that the current flow into or out of the smaller ``device''
represents a negligible perturbation. The reservoirs represent the metallic contacting
leads to discrete devices or experimental samples, or the power-supply busses at
the system level. Consequently the electrons flowing from from a reservoir into the
device occupy that equilibrium distribution which characterizes the reservoir. In
a simple one-dimensional system with two reservoirs, the electrons flowing in from
the left-hand reservoir have k > 0 and those flowing from the right-hand
reservoir have k < 0.
Within this picture, the current that is injected from the left-hand reservoir is
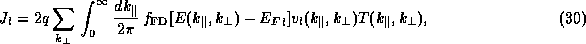
and the current injected from the right-hand reservoir is
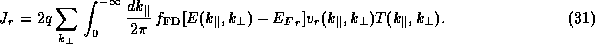
In order to simplify the calculation of
J further, we must invoke some special properties of the system. The most useful
such property is that symmetry which permits the separation of the spatial variables.
The separation of variables is possible if the Hamiltonian can be separated into
two parts:
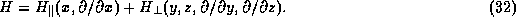
(Here the notation 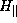 and
and 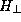 is defined with respect to the direction
of current transport.)
Then the wavefunction separates into a product of two factors:
is defined with respect to the direction
of current transport.)
Then the wavefunction separates into a product of two factors:

and the energy can be separated into a product of two terms:

The expression for the total current density J can now be simplified to
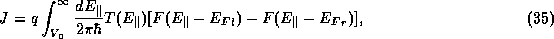
where 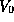 is the larger of the two asymptotic potentials (minimum energy for a
propagating state) and F is the Fermi-Dirac distribution function summed over the transverse states:
is the larger of the two asymptotic potentials (minimum energy for a
propagating state) and F is the Fermi-Dirac distribution function summed over the transverse states:

The form of the sum over 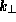 depends upon the spatial configuration of the
tunneling system. Note that the velocity factor does not appear in (35)
because it was canceled by the density of states.
depends upon the spatial configuration of the
tunneling system. Note that the velocity factor does not appear in (35)
because it was canceled by the density of states.
If the system in question is macroscopically large in its transverse dimensions,
the 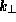 form a two-dimensional continuum, and
form a two-dimensional continuum, and
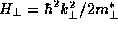 . Then using the two-dimensional analog of
(22) and (25) F can be analytically evaluated:
. Then using the two-dimensional analog of
(22) and (25) F can be analytically evaluated:

The current density can now be written in the form usually given for the tunneling
current [10]:
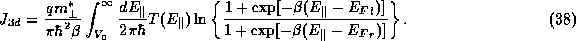
Note that this expression is valid in general with respect to the dispersion relation
in the x direction, but requires a parabolic dispersion relation in the transverse
directions. The separation of variables leading to (38) is never
rigorously valid in a semiconductor heterostructure. The reason for this is that the
transverse effective mass 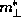 will vary with semiconductor composition, which
varies in the x direction. In principle, one must do at least a two-dimensional
integral (if axial symmetry holds, otherwise a three-dimensional integral) as implied by
(2). Nevertheless, (38) is widely used to
model the current density in heterostructure devices. The error introduced by
assuming separation of variables is probably less severe than that due to the assumption
of an infinite coherence length.
will vary with semiconductor composition, which
varies in the x direction. In principle, one must do at least a two-dimensional
integral (if axial symmetry holds, otherwise a three-dimensional integral) as implied by
(2). Nevertheless, (38) is widely used to
model the current density in heterostructure devices. The error introduced by
assuming separation of variables is probably less severe than that due to the assumption
of an infinite coherence length.
If the transverse dimensions are constrained, but separation of variables is still
possible, the transverse motion of the electrons consists of a discrete set of standing
waves or normal modes. Such systems are referred to as ``one-dimensional'' systems,
quantum wires, or electron waveguides. The symbol 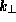 is now interpreted as
an index for the discrete transverse modes, and the expression for the current
density now becomes
is now interpreted as
an index for the discrete transverse modes, and the expression for the current
density now becomes
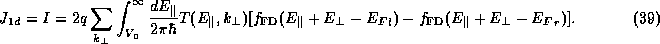




Next: Evaluation of Scattering-State
Up: Tunneling Theory
Previous: General Formulation
William R. Frensley
Fri Jun 23 15:00:21 CDT 1995
 -function
normalization, the derivation of the correct expressions are rather tricky, because
we seek expressions for densities of charge, current, energy, etc., rather than total
quantities (which are of course infinite in an unbounded system). To illustrate
the procedure, let us follow through the derivation of the electron density in
a spatially uniform three-dimensional semiconductor in equilibrium. We approximate
the conduction band structure by a simple parabolic dispersion relation:
-function
normalization, the derivation of the correct expressions are rather tricky, because
we seek expressions for densities of charge, current, energy, etc., rather than total
quantities (which are of course infinite in an unbounded system). To illustrate
the procedure, let us follow through the derivation of the electron density in
a spatially uniform three-dimensional semiconductor in equilibrium. We approximate
the conduction band structure by a simple parabolic dispersion relation:

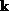 is the wavevector. The probability that each state
is the wavevector. The probability that each state 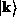 will be occupied by an electron is given by the Fermi-Dirac distribution function:
will be occupied by an electron is given by the Fermi-Dirac distribution function:
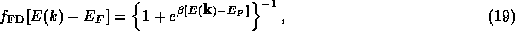
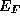 is the Fermi level or chemical potential and
is the Fermi level or chemical potential and 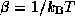 , T
being the absolute temperature. (To avoid confusion with the transmission probability
which is also denoted by T, the absolute temperature will always be shown
multiplied by Boltzmann's constant
, T
being the absolute temperature. (To avoid confusion with the transmission probability
which is also denoted by T, the absolute temperature will always be shown
multiplied by Boltzmann's constant  .)
Let us now
make an ad hoc assumption that the semiconductor crystal is a cube with each
side of length L, and
apply periodic boundary conditions. Then the stationary quantum states are plane
waves (normalized to unit amplitude) of the form
.)
Let us now
make an ad hoc assumption that the semiconductor crystal is a cube with each
side of length L, and
apply periodic boundary conditions. Then the stationary quantum states are plane
waves (normalized to unit amplitude) of the form

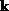 must assume discrete values:
must assume discrete values:
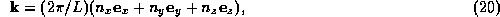
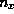 ,
, 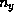 , and
, and 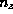 are integers. The total number of electrons in the
crystal N is just the sum over all of the states
are integers. The total number of electrons in the
crystal N is just the sum over all of the states 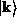 of the probability
that each state is occupied
of the probability
that each state is occupied

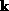 are very closely spaced, and the sum over
are very closely spaced, and the sum over 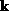 can be well
approximated by an integral:
can be well
approximated by an integral:

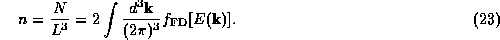
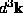 in spherical coordinates and
manipulating the dispersion relation (
in spherical coordinates and
manipulating the dispersion relation (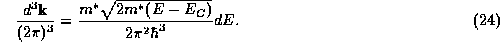
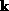 vectors. For the two-dimensional case (still
assuming a parabolic dispersion relation):
vectors. For the two-dimensional case (still
assuming a parabolic dispersion relation):


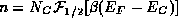 .
.
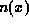 and the current
density j (which is independent of position in one dimension and steady-state).
The expectation value of the density for a state
and the current
density j (which is independent of position in one dimension and steady-state).
The expectation value of the density for a state 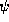 is simply
is simply

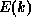 is not parabolic and independent of position, the form
of the operator j is not given by the simple textbook expression
is not parabolic and independent of position, the form
of the operator j is not given by the simple textbook expression
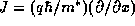 . The current density operator is
instead whatever remains of the kinetic energy term of the Hamiltonian after
the application of Green's identity as in the derivation of (
. The current density operator is
instead whatever remains of the kinetic energy term of the Hamiltonian after
the application of Green's identity as in the derivation of (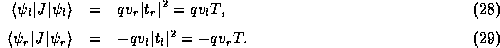
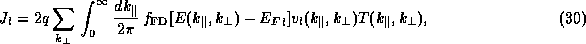
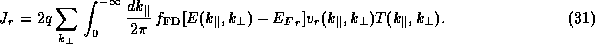
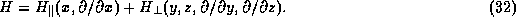
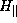 and
and 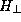 is defined with respect to the direction
of current transport.)
Then the wavefunction separates into a product of two factors:
is defined with respect to the direction
of current transport.)
Then the wavefunction separates into a product of two factors:


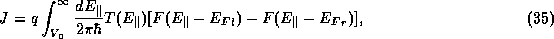
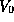 is the larger of the two asymptotic potentials (minimum energy for a
propagating state) and F is the Fermi-Dirac distribution function summed over the transverse states:
is the larger of the two asymptotic potentials (minimum energy for a
propagating state) and F is the Fermi-Dirac distribution function summed over the transverse states:

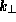 depends upon the spatial configuration of the
tunneling system. Note that the velocity factor does not appear in (
depends upon the spatial configuration of the
tunneling system. Note that the velocity factor does not appear in (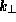 form a two-dimensional continuum, and
form a two-dimensional continuum, and
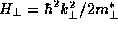 . Then using the two-dimensional analog of
(
. Then using the two-dimensional analog of
(
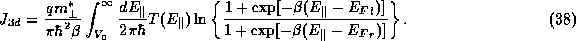
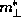 will vary with semiconductor composition, which
varies in the x direction. In principle, one must do at least a two-dimensional
integral (if axial symmetry holds, otherwise a three-dimensional integral) as implied by
(
will vary with semiconductor composition, which
varies in the x direction. In principle, one must do at least a two-dimensional
integral (if axial symmetry holds, otherwise a three-dimensional integral) as implied by
(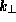 is now interpreted as
an index for the discrete transverse modes, and the expression for the current
density now becomes
is now interpreted as
an index for the discrete transverse modes, and the expression for the current
density now becomes