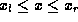To apply the above results to a given device structure, we need a method to
determine the transmission and reflection coefficients for any given energy.
These are determined by solving, either explicitly or implicitly, Schrödinger 's equation
over the domain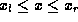 
. Again, we assume that outside this domain
(in the asymptotic regions),
the wavefunction consists of a superposition of traveling waves, and we write the
general solution
The task is to find the relation connecting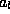 
, 
, 
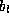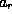, and 
.
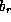The traditional, ``textbook,'' techniques for solving one-dimensional scattering
problems are the Wentzel-Kramers-Brillouin (WKB) approximation and the
transmission-matrix scheme [11]. In the WKB approximation, the
wavefunction is written as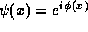 
, and semi-classical expressions
are developed for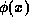 
. These require that the potential be slowly varying,
and thus are not particularly suited to the analysis of abrupt heterostructures.
In the transmission matrix approach the
domain is divided into a suitable number of intervals over each
of which the potential can be taken to be constant, or perhaps
linearly varying. Within each such interval, the wavefunction
is expanded in terms of the two independent solutions at the
chosen energy (oppositely directed traveling waves if the
potential is constant). Then the amplitudes of these waves at the two ends of
interval i can be related by a propagation matrix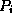 
:
The appropriate matching conditions at the boundary between intervals i and i+1
must be derived from the form of the Hamiltonian, and are expressed by a matrix
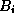which is typically of the form:
where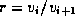 
, the velocity ratio. One can then relate the coefficients
in the left asymptotic region, incorporated into a vector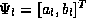 
, to
those in the right asymptotic region,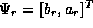 
, by a matrix M formed
from the product of the appropriate propagation and boundary matrices:
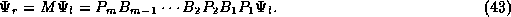
In practical calculations, the transmission matrix approach has proven to be less than satisfactory, because it is prone to arithmetic overflow. In regions where the wavefunction is evanescent, the P matrices contain real elements equal to the attenuation of the region and its inverse. The inverse is likely to be a very large number, and if several evanescent regions are cascaded, the numbers in the matrix will rapidly exceed the dynamic range of floating-point variables. This problem is particularly severe when the transmission matrix scheme is applied to multi-band models, because at any given energy many of the bands will be evanescent [12], but it has also been observed in simple single-band calculations [13].
A much more robust and effective scheme for solving Schrödinger 's equation involves
expanding the equation on a set of localized basis functions to reduce the
differential equation to
a set of linear algebraic equations, and directly solving those equations.
This approach is numerically faster, more stable,
and more readily applied to differing structures. One can take the basis functions
to be any set of localized functions: atomic s-orbitals, Wannier orbitals [14],
simple finite-element shape functions, etc., but, for one-dimensional models,
all such methods produce
similar sets of linear equations to be solved.
For the present purposes, let us consider the derivation
simply in terms of a finite-difference approximation to the
differential form of the effective-mass Schrödinger equation (1), in which
the effective mass may vary as a function of x. We assume that the wavefunction
is known only on a set of discrete points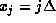 
, where 
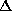is the
mesh spacing. The discrete values of the wavefunction will be denoted by
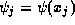. If the effective mass did
not vary, we could simply use the three-point approximation for the second derivative,
This reduces the Schrödinger equation to a set of equations of the form:
which can be written as a matrix equation with the Hamiltonian being a tridiagonal matrix.
When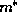 
is allowed to vary, the form of the equations is not changed, but this
variation must be taken into account in the values of the matrix elements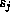 
,
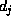. These values may be systematically derived from the variational principle
for Schrödinger 's equation [15]:
If we assume that the wavefunction varies in a simple fashion (such as linearly) between
mesh points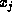 
, L can be readily evaluated in
terms of the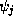 
and 
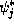, and the discrete Schrödinger equation derived by setting
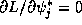for all j. The particular expressions obtained
for the matrix elements depends upon the detailed picture we assume for the functional
dependence of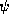 
and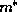 
within the interval between two adjacent meshpoints.
If we assume that the wavefunction varies linearly between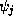 
and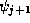 
,
and that the effective mass is constant across this interval with value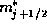 
,
one obtains [16]:
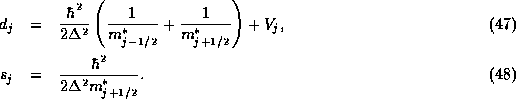
If the effective mass is constant across the mesh interval, one is effectively assuming that the heterojunctions occur on a mesh point, and there is a question of what value of the potential to assign to this point. In general, it is better to assume that the heterojunction occurs halfway between two adjacent mesh points. With this model for the spatial dependence of the effective mass, and still assuming linear variation of the wavefunction, the Hamiltonian matrix elements become:
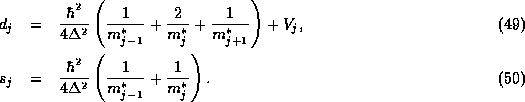
These expressions can be improved upon by taking into account the matching condition
on the wavefunction implied by the form of the continuous Hamiltonian (1),
which is that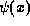 
and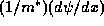 
are continuous across a
heterojunction. Assuming that the wavefunction is piecewise linear so as to
satisfy this condition between meshpoints yields the most accurate discretization
[17]:
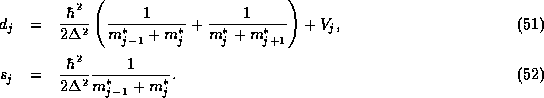
If one seeks the eigenstates of a closed system,
the tridiagonal Hamiltonian may be readily diagonalized by standard
numerical techniques. However, we are here concerned with the problem
of the scattering states in an open system. This requires that appropriate boundary
conditions be formulated and applied to (45). Lent and Kirkner
[18] have demonstrated how to do this in the context of a finite-element
electron waveguide calculation, and their approach is called the Quantum Transmitting
Boundary Method (QTBM). In the continuous case, one derives the QTBM conditions
by evaluating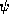 
and its derivative 
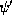at 
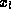and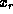 
using
(40).
One then solves for the incident amplitudes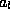 
and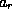 
in terms of 
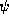and
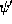, and imposes the resulting expressions upon Schrödinger 's equation as
inhomogeneous boundary conditions. Conditions of this type, in which a linear
combination of the function and its derivative are specified, are known as
Robbins conditions. They are implicit, in the sense that they must be solved
along with the differential equation itself. However, as we shall see below, this
presents no problem in a discrete, numerical approach.
In the discrete case,
it is simpler to express
the QTBM conditions as a linear combination of the values of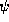 
on
two adjacent meshpoints. If the points j = 1 and j = n are the
limits of the domain in which the potential can vary, we may add
boundary points at j = 0 and j = n+1. The form of the wavefunction
will be taken to be:
where z is the propagation factor, and is equal to either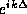 
for
propagating states or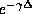 
for
evanescent states. The values of z at the boundaries
may be directly obtained by solving Schrödinger 's equation in the boundary
neighborhoods:
The wavefunctions near the boundaries may thus be written:
To obtain the QTBM equations, one solves (3) for
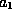and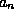 
, obtaining
Adding (3) to the matrix representation to Schrödinger 's equation (45) we obtain the linear system to be solved:
To find the left-incident scattering state one would simply set
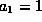and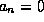 
(and conversely for the right-incident state) and
solve the tridiagonal system for all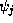 
. Because the matrix is tridiagonal,
a very fast numerical technique can be applied to its solution [19],
though complex arithmetic must be used.
This scheme provides an extremely simple and robust way to evaluate scattering-state
wavefunctions. It
has been applied to multi-band tight-binding calculations and has
solved the stability problems which have severely hampered transmission-matrix
calculations of similar problems [20]. It can also be adapted to the
problem of locating and characterizing resonant states [21]. The
eigenvalues of (63) give the resonant energy (real part) and the
resonance width (imaginary part). Because the 
and 
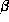elements of
(63) are energy-dependent, the eigenvalue problem is nonlinear and must
be solved by an iterative procedure. Also, the standard theorem stating that the number
of eigenvalues equals the dimension of the matrix no longer holds. An example of
a calculation using this technique is shown in Figure 1 which
shows the resonant states of a double quantum-well structure under bias.
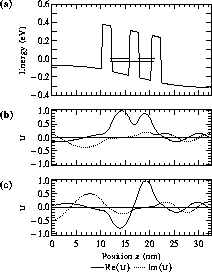
Figure 1: Resonant states of a double quantum-well structure under that
voltage bias which brings the resonances into alignment. The resonances were located
by finding the eigenvalues of (44). In (a) the conduction-band profile
is shown along with an indication of the energy and localization of the resonances.
The lower-energy resonant wavefunction is shown in (b) and the higher-energy resonant
wavefunction is shown in (c).
