
|
|
|
|
Stochastic Bayesian Inference
Bayesian inference is a powerful approach for integrating independent conflicting information for decision-making and robotics, performed with limited efficiency by general-purpose computers.
Excitingly, Bayesian inference can be performed extremely efficiently through stochastic computing with Muller C-elements.
This fault-tolerant circuit structure enables naive Bayesian inference with multiple orders of magnitude decrease in AEDP.
C-Element Bayesian Inference
The Muller C-element, characterized by the truth table below is a two-input memory element composed of eight transistors.
The output Z maintains its state Zprev unless both inputs X and Y are opposite the current output state, in which case the output switches to the shared input value.
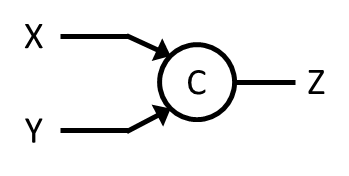

For C-element input signals with no autocorrelation, the output probability is given by the equation below.
This equation is equivalent to an inference based on Bayes' rule, demonstrating that with stochastic computing, a simple C-element performs a complete Bayesian inference.
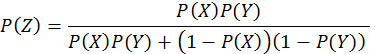
Example: Naive Bayesian Spam Filter
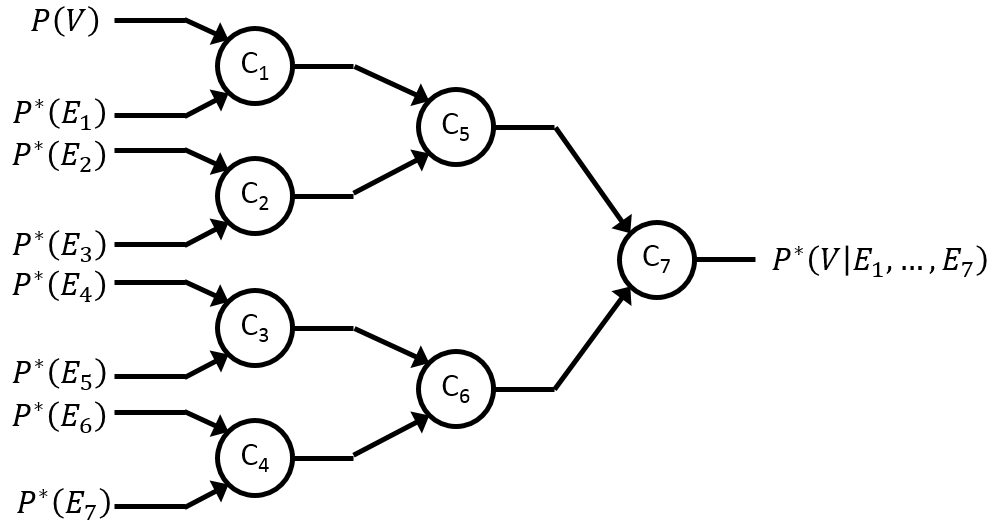
Multiple C-elements can be cascaded to perform complex inferences incorporating numerous independent sources of information.
This extends the stochastic inference described above, enabling the fusion of evidence inputs Ei to determine the probability of an event V.
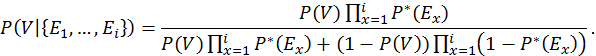
Spam filtering illustrates the capability of cascaded C-elements to perform a canonical Bayesian inference.
Consider the messages in the table below: A and B are likely to be ham (i.e., not spam), C is almost definitely spam, D seems to be ham but contains many words that are associated with spam, E is probably spam, and F is entirely ambiguous.
To infer the probability that a message is spam, a simple Bayesian spam filter considers the "spamicity" of key words in a message.
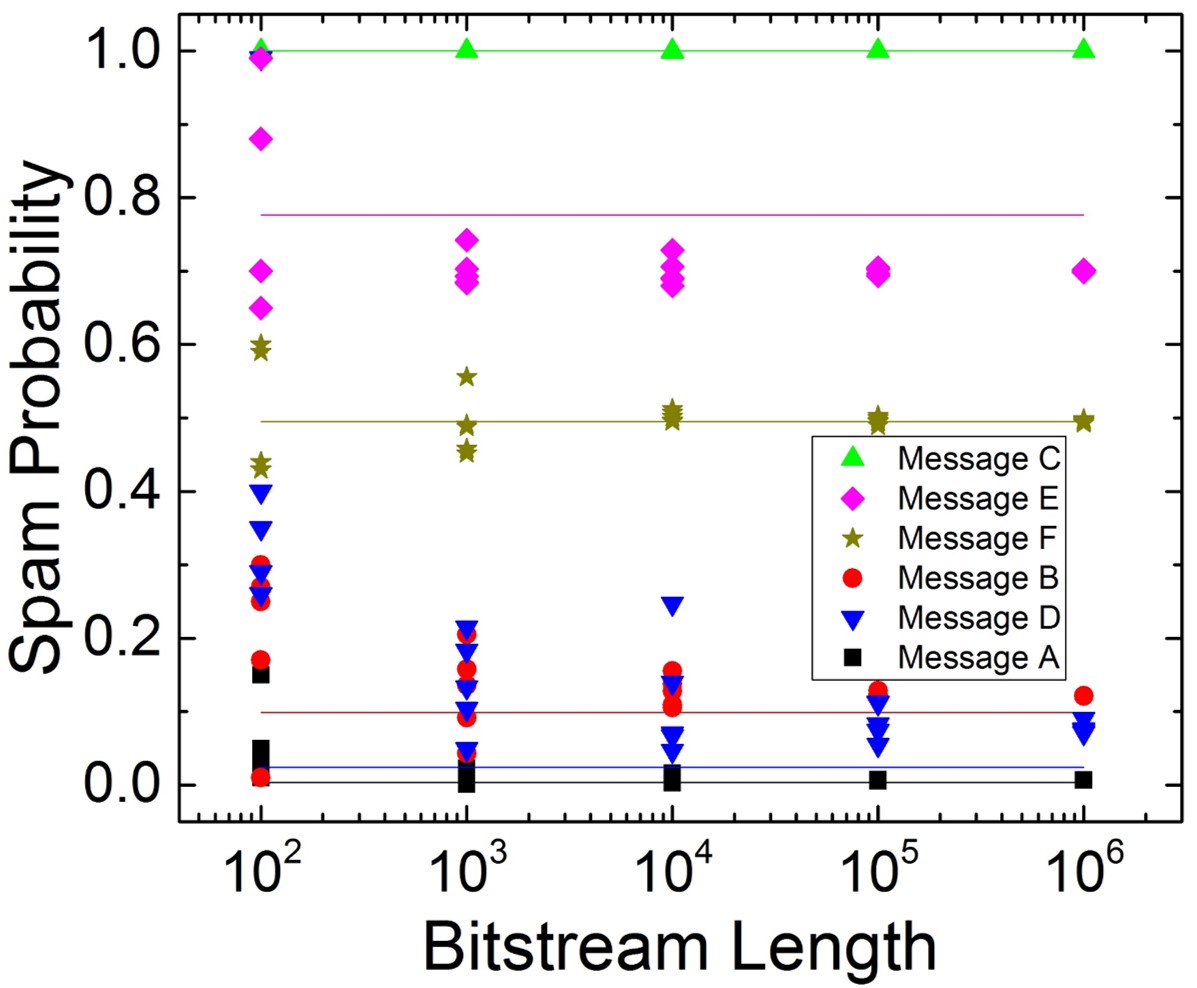
The three-stage C-element tree above can be used to perform the spam filter operation on messages A-F for eight key words.
The simulation results show that for increasingly long stochastic bitstreams, the stochastic circuit computes probabilities (dots) that approach the exact naive Bayesian inference (solid line).
This simple Bayesian system successfully filters the messages, with high outputs for message C and E, low outputs for messages A, B, and D, and an ambiguous output for F.

Efficiency & Fault Tolerance
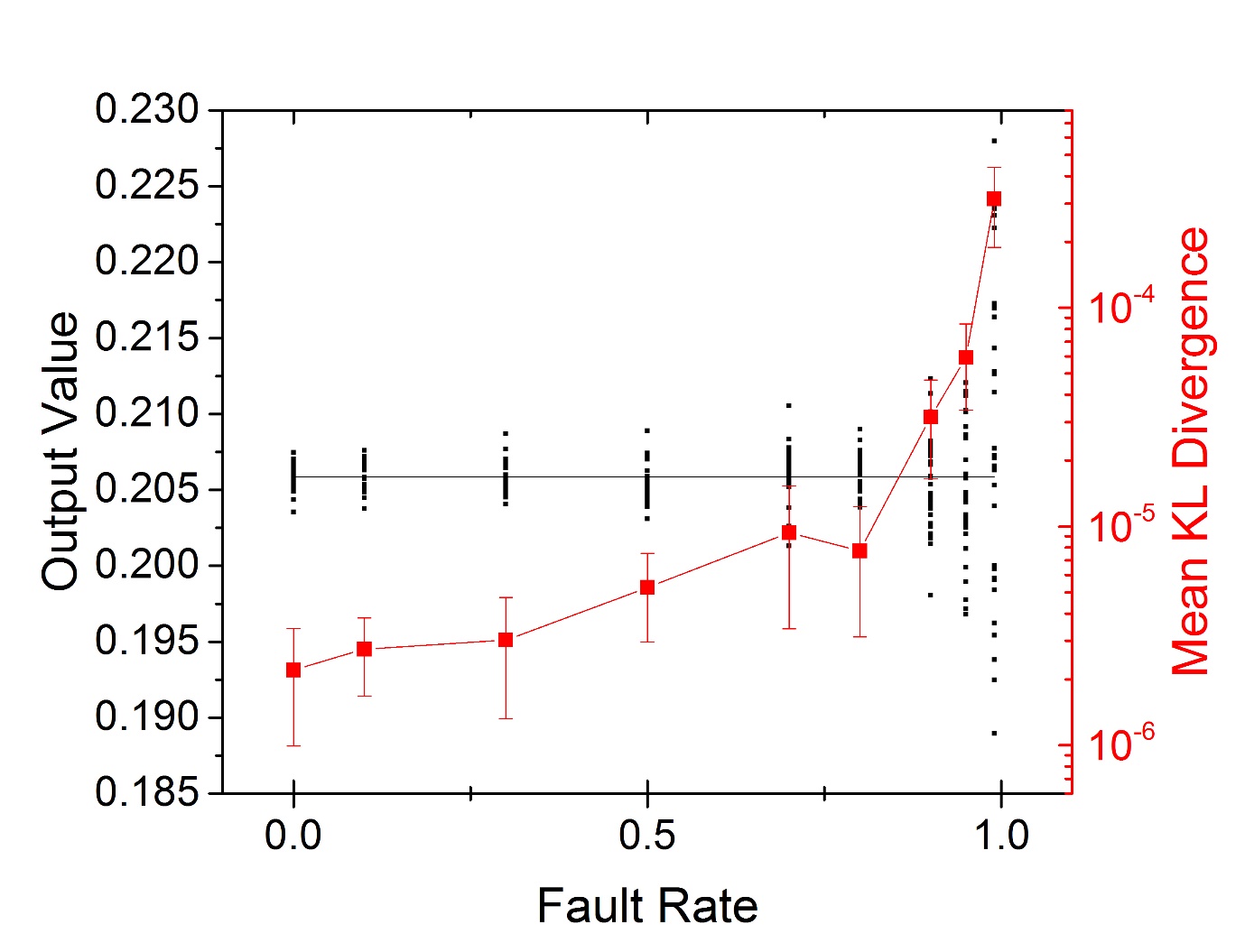
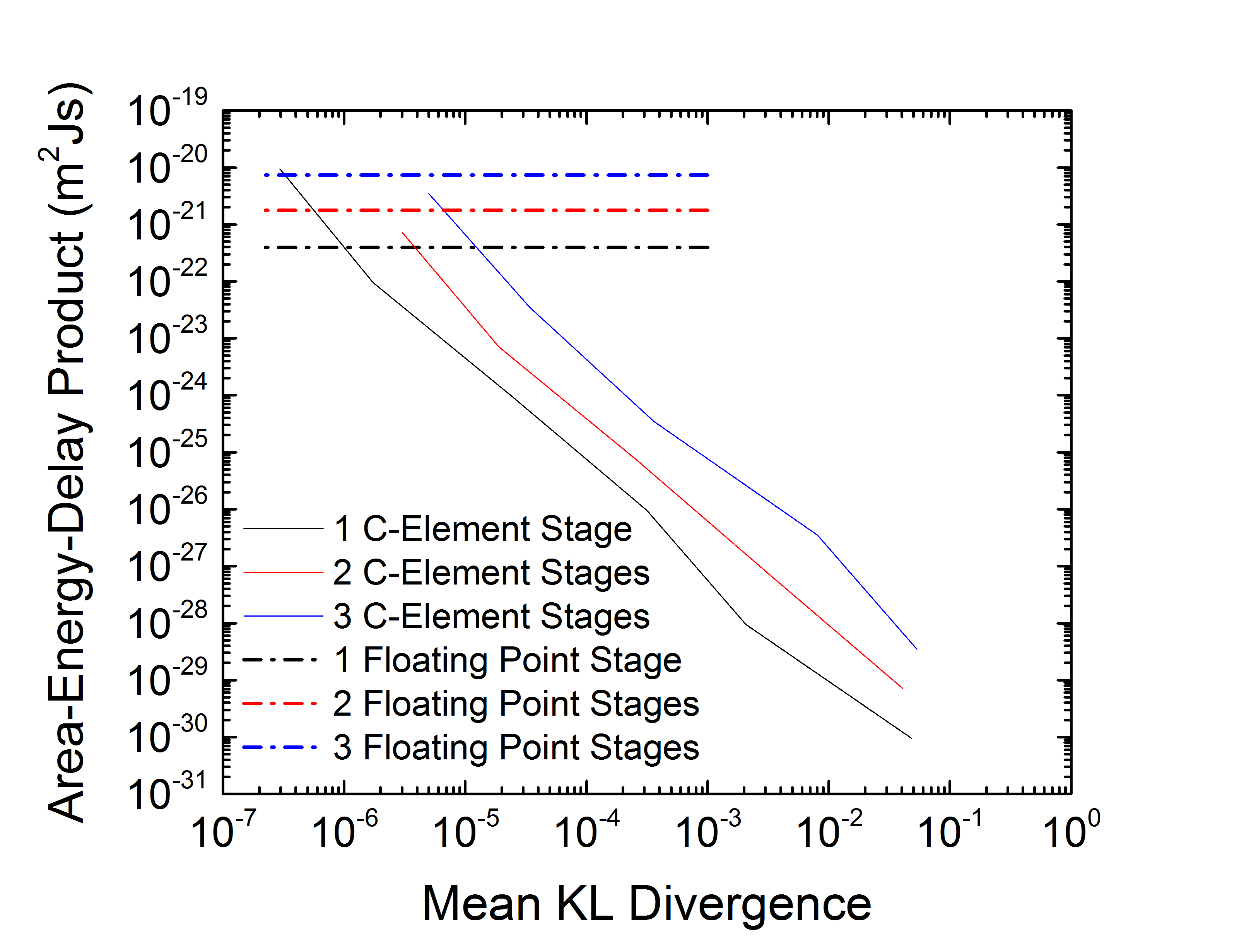
The primary benefits of this stochastic inference structure are exceptional efficiency and fault tolerance for applications that do not require exact solutions.
For an output KL divergence of 0.01 (sufficient accuracy for some practical applications), the stochastic inference circuit provides a area-energy-delay product (AEDP) decrease by a factor of nearly one billion!
The system is also extremely robust to faults, providing nearly perfect results for stuck-at fault rates of nearly 100%.
Related Publications
- A. J. Edwards, E. C. Usih, P. Zhou, B. A. Hill, S. Martindell, T. Qi, D. Biswas, X. Hu, S. M. Panduranga, J. S. Friedman, Experimental Demonstration of Stochastic Bayesian Inference using Muller C-Elements, Government Microcircuit Applications & Critical Technology Conference, Mar. 2024.
- D. Querlioz, A. F. Vincent, A. Mizrahi, D. Vodenicarevic, J. S. Friedman, N. Locatelli, J. Grollier, Neuromorphic Computing with Stochastic Spintronic Devices, Conference on Magnetism and Magnetic Materials, Nov. 2017 (invited).
- D. Vodenicarevic, N. Locatelli, A. Mizrahi, J. S. Friedman, A. F. Vincent, M. Romera, A. Fukushima, K. Yakushiji, H. Kubota, S. Yuasa, S. Tiwari, J. Grollier, D. Querlioz, Low-Energy Truly Random Number Generation with Superparamagnetic Tunnel Junctions for Unconventional Computing, Physical Review Applied 8, 054045 (2017).
• Featured by nanotechweb
- D. Querlioz, A. F. Vincent, A. Mizrahi, D. Vodenicarevic, N. Locatelli, J. S. Friedman, J.-O. Klein, J. Grollier, Neuromorphic Computing with Stochastic Spintronic Devices, SPIE Spintronics, Aug. 2017 (invited).
- J. S. Friedman, J. Droulez, P. Bessière, J. Lobo, D. Querlioz, Approximation Enhancement for Stochastic Bayesian Inference, International Journal of Approximate Reasoning 85, 139-158 (2017).
- L. E. Calvet, J. S. Friedman, D. Querlioz, P. Bessière, J. Droulez, Sleep Stage Classification with Stochastic Bayesian Inference, IEEE/ACM International Symposium on Nanoscale Architectures, July 2016.
- J. S. Friedman, L. E. Calvet, P. Bessière, J. Droulez, D. Querlioz, Bayesian Inference with Muller C-Elements, IEEE Transactions on Circuits & Systems I 63:6, 895-904 (2016).
- J. S. Friedman, L. E. Calvet, P. Bessière, J. Droulez, D. Querlioz, Bayesian Inference with Muller C-Elements, IEEE International Symposium on Circuits & Systems, May 2016.
|




