$(\pi+2)$-Day: Buffon's Noodle

Maxim Arnold and Nathan Williams
Department of Mathematical Sciences
University of Texas at Dallas
$\pi$: the ratio of the circumference of a circle to its diameter.

Mathematics: an Experimental Science
In 1773, Georges Louis Leclerc, le Comte de Buffon devised a mathematical experiment...

Buffon's Needle
To perform this experiment at home, you'll need:
- Needles. (Preferably substitute something less sharp.)
- A grid of equally spaced parallel lines (unit distance apart).


Buffon's Needle
How often does a randomly tossed needle cross a line?
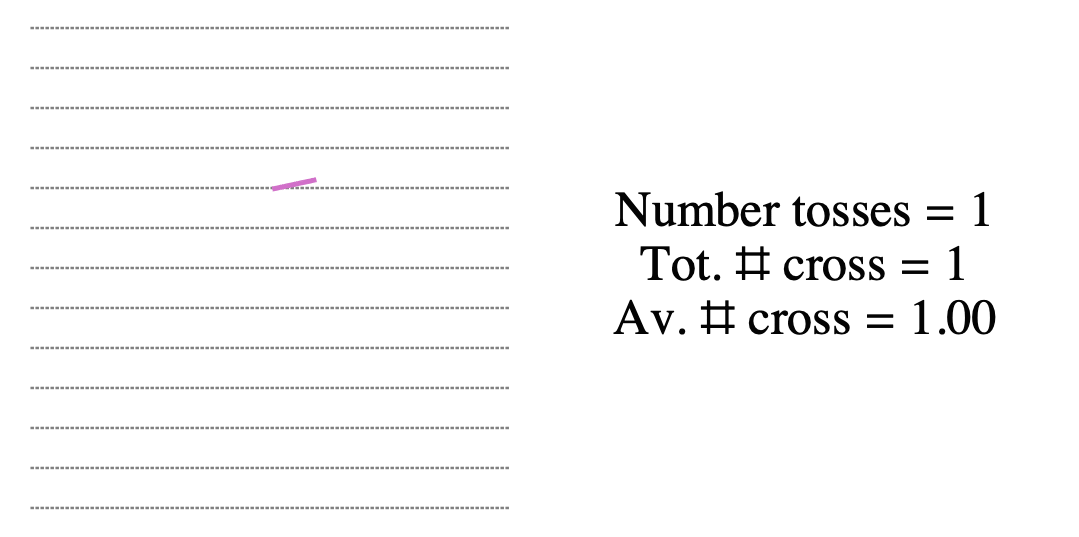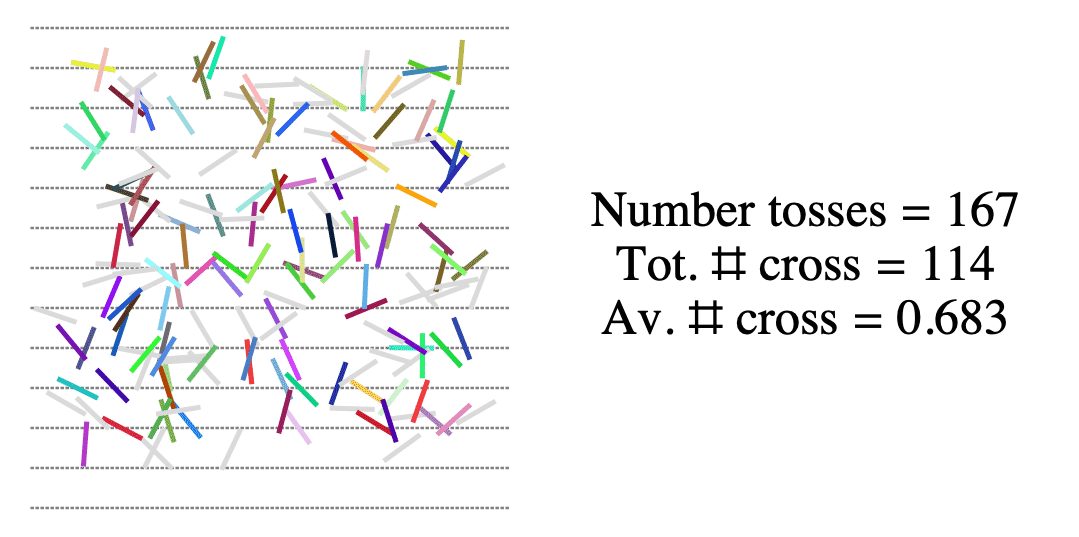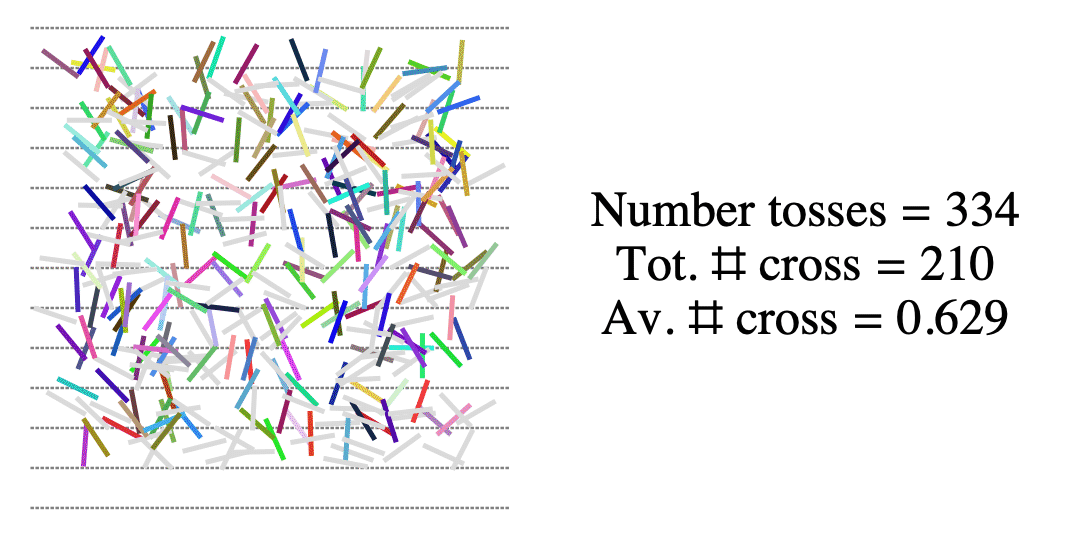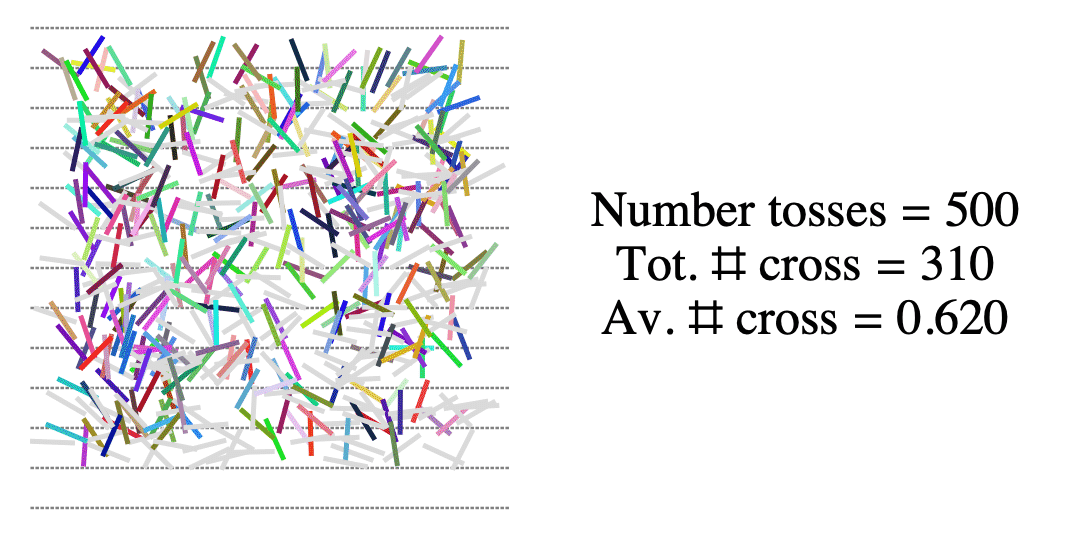
Now compute
\[\frac{2}{\text{average number of crossings}} \approx \frac{2}{E}\]

Now compute
\[\frac{2}{\text{average number of crossings}} \approx \frac{2}{E} = \pi?\]

Buffon's Needle
By breaking a needle in two, one checks that \[E=C \ell,\] where $\ell$ is the length of the needle and $C$ is some constant.

Buffon's Noodle
$E=C\ell$ only depends on $\ell$, and doesn't change for a "noodle".

Buffon's Noodle
$E=C\ell$ only depends on $\ell$, and doesn't change for a "noodle".

Buffon's Noodle
$E=C\ell$ only depends on $\ell$, and doesn't change for a "noodle".

Use a circular noodle of unit diameter.


Use a circular noodle of unit diameter.
The length $\ell$ of such a noodle is our definition of $\pi$.
Such a noodle will always have exactly two intersections:

We conclude that if $\ell=1$
\[\frac{2}{\text{average number of crossings}} \approx \frac{2}{E} = \frac{2}{C\ell} = \frac{2}{\pi/2} = \pi.\]

Other values of $\pi$...

Other values of $\pi$...

How to compute (digits of) $\pi$?
Approximating $\pi$ using Buffon's needles is slow. There are more efficient ways....
- Inscribe/circumscribe regular polygons in a circle.
- Infinite series.

Some famous formulas
\[ \frac{\pi}{4} = \sum_{k=1}^\infty \frac{(-1)^{k+1}}{2k-1} = 1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots\]
\[ \pi = \sum_{k=0}^\infty \frac{1}{16^k} \left( \frac{4}{8k+1}-\frac{2}{8k+4}-\frac{1}{8k+5}-\frac{1}{8k+6}\right)\]
\[ \frac{\pi}{2} = \frac{ 2\cdot 2 \cdot 4 \cdot 4 \cdot 6 \cdot 6 \cdots}{ 1\cdot 3 \cdot 3 \cdot 5 \cdot 5 \cdot 7 \cdots}\]
\[ \frac{2}{\pi} = \frac{\sqrt{2}}{2}\cdot \frac{\sqrt{2+\sqrt{2}}}{2}\cdot \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \cdots\]
Thank you!

Use a spacebar or arrow keys to navigate