Waves Matter

Chm 1311 Lectures for 14 June 2000

Electro- magnetic Radiation James Clerk Maxwell MS Encarta '97	Is there any other kind? Sure! We're constantly under bombardment by neutrino radiation (remember the Updike poem?). And when radioactive nuclei decay, out may pop helium nuclei called a radiation. And we might see sprays of electrons called b radiation. But the other biggy for radioactive decay is g radiation, and that is electromagnetic. The other things you associate with radiation, from the glow of embers in a fire to light from the most distant galaxies, is electromagnetic as was explained by James Clerk Maxwell over a century ago. His famous four equations of electricity and magnetism implied the mutual propagation of oscillating electric and magnetic fields (changing electric fields make magnetism - witness an electromagnet - while changing magnetic fields make electricity - witness electric generators). As long as these fields were perpendicular to one another, they merrily recreated one another off to infinity...or until they were absorbed by matter. Those mated fields were light, and their sinusoidal oscillations explained all of last century's interesting light properties, such as diffraction (rainbows) and reflection (mirrors). Yes, light was definitely a wave. 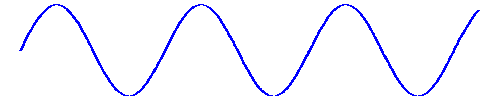And the spacing between peaks was the "wavelength" symbolized by l. And as it travelled past you, the time between peaks was the "period" symbolized by t. And since the velocity of anything is the distance travelled, l, in a given time, t, the velocity of the wave, that is, the speed of light, is obviously v = l/t.
The Speed of Light Albert Einstein MS Encarta '97	More useful for our discussions, however, is not the period (time between peaks as they pass) but rather the frequency, n, how many peaks pass in one second. Not surprisingly, n = 1/t which makes that speed calculation read c = n l instead. Since the speed of light isn't just any old velocity, it's given its own symbol, c, instead of just the v for velocity. c is special as a velocity since Einstein positted that nothing can exceed the speed of light. You might think that at c = 3×108 m s-1 nothing would need to exceed the speed of light, but NASA would like to. It would permit exploration of other solar systems in a person's lifetime, but even at the speed of light, the nearest star, a Centuri, is a 9 year round trip away. That's a lot of Twinkies and Coke! Relativity aside, we have a simple way of converting between the wavelength and the frequency of light, viz., l = c/n and vice versa. That's important because spectroscopic measurements of light are made in wavelength, but energy of light is proportional to its frequency!
Planck's Equation Max Planck MS Encarta '97	That latter was the revelation of Max Planck, immortalized nowadays in the seemingly hundreds of Max Planck Institutes of science in Germany. Planck was trying to fix a theoretical error (in light intensities from hot objects) and discovered that instead of being a wave of continuously varying magnitude (intensity), light actually was born and died as a particle (photon) with precisely the energy hn! And that proportionality constant, h=6.626×10-34 J s, is today called "Planck's Constant". This relation and the prism (or diffraction grating) which casts white light into its components with known wavelengths bent by known angles, give us the tools we need to peer into the inner workings of atoms! Not merely check their size (atomic microscopy) but rather determine experimentally their internal energy states! How? By giving them a kick and seeing what light falls out. And the kicker is that the light that falls out is not smeared out over many wavelengths but rather concentrated into several lines in atomic spectra. Those lines mean incredibly precise energy differences between atomic states since any energy the atom loses, the photon gains (by conservation of energy).
Hydrogen Spectrum The visible lines in the spectrum of hydrogen. (The violet line is very weak.) Niels Bohr	We saw those lines for hydrogen in class with our own spectrometer and confirmed that their wavelenths conformed to Rydberg's formula, l = 1 / [ RH ( 2-2 - n-2 ) ] for n > 2 The simplest possible energy levels scheme which would result in those wavelengths would be E = - hcRH / n2 for n=0,1,2,... where we've used both Planck's equation and that reciprocal relation between wavelenght and frequency. The beauty of this expression (besides its wonderful simplicity) is that Niels Bohr was able to derive if from the attraction of an electron for a proton merely by presuming that not only energy came in discrete states (n isn't continuous but an integer) but so did angular momentum. We won't track his achievement here (but it's not hard to follow). And Bohr's development also worked for He+, Li2+, Be3+, etc. ... all the ions with only one electron on them! But nothing else. Bummer.
Multi- electron Atoms	The problem is there's more going on in a multi-electron atom, and it's not just that more electrons are attracted to the same nucleus. The problem is that they are repelled by one another! Much harder to deal with. But not the worst Bohring failure: the hardest part was that electrons just weren't little charged particles flying around in trajectories as Bohr assumed. They were instead smeared out into waves! This was first guessed by deBroglie who prediced that a "matter wave" would have a wavelength inversely proportional to its momentum, l = h/mv, where (lo and behold) the constant of (inverse) proportionality turned out to be Planck's!!! (Of course it's not a coincidence.)
Matter Waves	Davisson and Germer proved deBroglie was right by accelerating electrons onto a crystal and observing wave diffraction, as would be seen with X-rays, of the electrons when their wavelengths were comparable to the crystal spacings! And now all freshman chemistry professors are stuck trying to get their students to believe that electron particles are really electron waves. Nobel Laureate Richard Feynman said it best when he suggested "Do not keep saying to yourself, if you can possibly avoid it, 'But how can it be like that?' because you will get 'down the drain' into a blind alley from which nobody has escaped. Nobody knows how it can be like that." In essence, all matter gets where its wave can go but appears as a particle when it gets there. Until it gets there, it is wherever its (diffuse) matter wave is. Worse still, it makes its own matter wave, like God surfing. So even though that's screwy...because nothing in our day-to-day world acts that way, it is nonetheless true of atomic sized things. These matter wave phenomena don't trouble us non-atomic critters because our masses are so large that our deBroglie wavelengths vanish well below the dimensions of a nucleus let alone an atom! Such small wavelengths don't diffract on anything, so none of us ever spontaneously breaks up into a rainbow. Pity; sounds like fun.
Electron Orbitals	Ok...if electrons don't "orbit" their nuclei, what paths do they take? Wrong question. It presumes particle thinking. OK OK ... if they don't orbit, where in the atom are they? Better question...as long as you're willing to accept an answer as fuzzy as the breadth of a wave! Electron waves, like light waves, have nodes, but while light is in constant motion (c), electrons trapped in atoms are stationary waves with fixed nodal patterns.
n is the Principal Quantum Number	That integer n from the Rydberg equation turns out to govern the lion's share of all electronic energy by being (one more than) the number of nodal surfaces in the wave. Why should that influence energy? Because more nodes mean shorter wavelengths, and shorter wavelengths mean bigger momenta (deBroglie), and bigger momenta mean bigger kinetic energies! Voila.
	And since the number of nodes is n-1, the smallest n (1) implies the fewest nodes possible is zero. Too true. But where are these nodes? To begin with, they are radial surfaces within the electron matter wave (centered on the nucleus) where the wave has zero amplitude. If n=3, there are n-1=2 such spherical nodes, but for n=1, there's none at all, and that matter wave just dies out as one walks away from the nucleus.
l is the Angular Quantum Number	But couldn't nodes be on planes as well as spheres? If so, they'd be angular nodes 'cause you wouldn't see them walking away from the nucleus but rather around it! Since nodes have to be either spherical or angular, we get a second quantum number, l (lowercase "L"), which is the number of these n-1 nodes that are angular. Since we can't have more angular nodes than there were nodes in the first place, l can never exceed n-1. But it can take on any integer value from 0 to n-1 meaning that the number of angular nodes can be from none to all of them.
ml is the Magnetic Quantum Number	Finally, the detailed geometry of the angles at which the nodes lie is determined by yet a third quantum number, ml. It's name as the magnetic quantum number comes from its being the direction that the electron's angular momentum points. Revolving charges (an electron with angular momentum about the nucleus) must generate magnetic fields (Maxwell) and their direction up (plus values), down (minus values), or perpendicular to (zero value) some external magnetic field would be energetically different...just as orienting two bar magnetics near one another, you can feel their attractions and repulsions! ml is actually the (quantized) shadow (projection) of the electron's angular momentum, l, along that imaginary external magnetic field. In a vector sense, ml is l's component along that direction. Since the component can never be larger than its vector, ml never exceeds l and never projects more negative than - l. Thus, ml takes on the 2l+1 integer values from - l to + l.
ms is the Spin Quantum Number	Finally, electrons all have one more quantum number which describes not their revolution about the nucleus (that would be l) but rather their rotation about themselves. They spin! (Why they spin has to do with Einstein's prohibition that nothing travels faster than light. If l=0, the electron has no angular momentum and should be able to fall into the nucleus. But it's infinitely attracted there as its distance to the nucleus goes to zero. Infinitely negative potential energy has to be balanced by infinitely positive kinetic energy, requiring infinite speeds! Sorry, says Einstein, c is the speed limit; you'll have to go around the nucleus not through it. ms is the angular momentum that the electron carries with it to avoid having to go through!)
	ms can take on only two values, +½ and -½. Fortunately, as it flips from one value to the other, the change in its angular momentum is one unit, the quantal minimum for angular momentum.
Pauli Principle	The importance of ms in Chemistry comes when one knows what Pauli knew: no two electrons in the same atom can have the same set of quantum numbers: n, l, ml, ms. The roots of this one are too deep to play with here (having to do with electron exchange symmetries), so we'll merely believe. However, it is probably the single most important reason why we exist at all! We are creatures of Chemistry. Chemistry is a creature of the wonderful differences between atoms. If the Pauli Principle were false, all atoms would be the same chemically and they'd never bond to make molecules! No molecules? No Life!
The Periodic Table	That Life-giving complexity of the atoms is celebrated in the Periodic Table. To the beginning student, the Periodic Table is a boon because it simplifies the welter of atoms by collecting them in chemically similar Groups (columns). What we can do now, with these four quantum numbers which uniquely characterize each of an atom's electrons, is show how the Periodic Table arises as a natural consequence of matter waves.