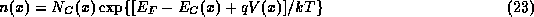
In a heterostructure, the band structure necessarily varies with position. This variation requires that the drift-diffusion equation for the current density be modified. This is most easily demonstrated by considering the case of thermal equilibrium, where the total current density must be zero. If the electron density is non-degenerate it may be approximated by the Boltzmann distribution:
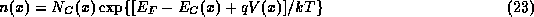
If we insert this into the ordinary expression for the diffusion current, we obtain an expression which must equal the negative of the drift current:
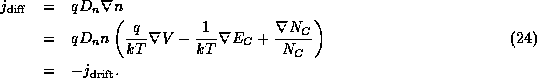
The effective density of states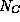 
depends upon position
through the effective mass 
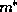, which is a function of the semiconductor
composition. Thus, from eq. (13) for parabolic bands,
Adding the drift and diffusion currents together, and making use of the Einstein relationship, we find that the electron current must be given by an expression of the form
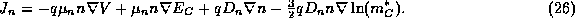
By a similar argument one obtains an expression for the hole current:
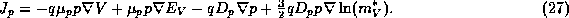
The first and third terms of eqs. (1) are the usual
drift and diffusion, respectively. The second and fourth terms are due
to the spatial variability of the band structure. The second term resembles
the drift term, but describes the carriers' response to changes in the
band-edge energy, rather than to changes in the electrostatic potential.
This effect is called a ``quasi-electric field'' [45], and is
the origin of much of the usefulness of heterostructures. This term is
readily understood on the basis that the carriers respond to gradients in
the total band-edge energies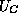 
and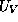 
. The fourth
term is more closely related to the diffusion term, and it describes the
dynamical effects of a variable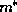 
. To visualize this effect, consider two materials,
having different effective masses but equal potentials and equal
temperatures, in intimate contact. The thermal energies in each material
are equal, but the average thermal velocity will be larger in the material
with the smaller 
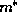. Those carriers will diffuse across the
interface between the materials faster than the heavier carriers, leading
to a net flux of particles out of the region of smaller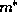 
. The
heterostructure drift-diffusion equations (1) may
also be derived microscopically, starting from the Bolzmann equation
[46]. Equations (1) may
also be written more compactly as
which is a more convenient form for subsequent manipulations.
Equations (1) may be solved analytically for the case
of steady-state transport in one dimension, provided that recombination and
generation may be neglected. The current density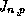 
will then be
independent of x. The carrier densities may be rewritten in
terms of the quasi-Fermi levels, or, equivalently, one multiplies the
drift-diffusion equation by an appropriate integrating factor. Let us
consider the electron current first. Recognizing
that both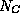 
and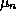 
(and thus 
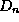) will be functions of the
position x, the integrating factor is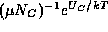 
.
Multiplying both sides of (28) by this factor and
integrating between points x = a and x = c, where the electron density
is presumed to be fixed, we find
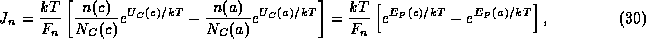
where
The drift-diffusion equation for holes may be similarly solved to yield
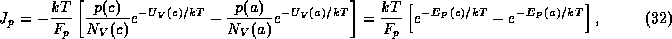
with
This solution is mathematically valid even when there are discontinuities
in the parameters such as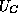 
. It thus provides a convenient way to
deal with abrupt heterojunctions. If one takes a and c to bound a
differential element centered upon an abrupt heterojunction, one finds
(not surprisingly) that the quasi-Fermi level should be continuous through the
heterojunction.
Equations (1) may also be used in numerical simulations,
to evaluate the current density between discrete mesh points.
The heterostructure drift-diffusion equations (1)
and their solutions (1) can be incorporated into the
conventional pn junction
theory to obtain expressions for the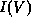 
characteristics of a heterojunction.
The variety of band alignment topologies makes it difficult to write generally
valid expressions. However, the general behavior of heterojunctions is easy
to understand intuitively and to describe (neglecting the broken-gap or extremely
staggered cases).
The barrier for carriers in the
wider-gap semiconductor to pass into the narrower-gap one is lowered as compared to
the barrier for carriers to pass from the narrower-gap material to
the wider-gap one. Thus the great majority of the forward current in a
heterojunction consists of one type of carrier, or in the language of bipolar
transistors, the injection efficiency is quite large. This effect is
exploited in the heterojunction bipolar transistor (HBT)
[4,3].
Equations (1) also provide a model for the rather common
case of current transport over an energy barrier. Suppose that 
has a maximum in the interval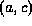 
at x= b. Then, because of the
exponential dependence upon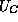 
, most of the contribution
to the integral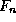 
will come from the vicinity of the barrier at b.
One may define an effective width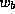 
for the barrier as that value
such that
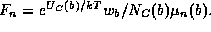The current density then becomes
This demonstrates the exponential dependence upon applied voltage (through
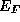) expected for barrier-limited current flow. If one considers very
narrow barriers, the factor of 
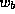in the denominator leads to a very large
pre-exponential factor. In such a case the energy band profile resembles that
of a Schottky barrier, and the drift-diffusion equation is not the most appropriate
model for current flow.
