



Next: Summary
Up: Irreversible Processes and
Previous: The Wigner Distribution
A more sophisticated approach to quantum transport theory is supplied by the
Green's-function formulation of many-body theory. This approach had its origins
in the development of the theory of quantum electrodynamics in the late 1940's and
early 1950's, and inherits this field's emphasis on perturbation expansions described
in diagrammatic form. The non-equilibrium Green's-function theory
was formulated by Kadanoff and Baym [59] and by Keldysh [60], was
elaborated by Langreth [61], and is described in the text by Mahan
[62]. The problems and promise of applying
this approach to electron devices has been discussed by Jauho [63].
In particular, most of the development of the Green's function approach has assumed
uniform electric fields, which is not adequate for the description of quantum devices.
Among the more recent work in this area which addresses problems beyond the uniform
field are those of Sols [64] and Rammer [65].
The non-equilibrium Green's functions are defined as expectation values of
single-particle creation and annihilation operators, and they describe the state and
time evolution of the system. There are four independent functions which appear in
the formalism. In the conventional notation 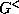 gives the distribution of electrons
(and reduces to the density matrix or Wigner function in certain limits),
gives the distribution of electrons
(and reduces to the density matrix or Wigner function in certain limits), 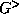 gives
the distribution of holes,
gives
the distribution of holes, 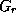 describes time evolution into the future and
describes time evolution into the future and 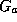 describes time evolution into the past. These Green's functions are determined by
solving a set of Dyson equations (an integral form of Schrödinger 's equation) which
form a convenient starting point for the development of a perturbation expansion.
describes time evolution into the past. These Green's functions are determined by
solving a set of Dyson equations (an integral form of Schrödinger 's equation) which
form a convenient starting point for the development of a perturbation expansion.
Each of the Gs has two position and two time arguments, which can be transformed
via the Wigner-Weyl procedure into one each of a position, momentum, time, and
energy (or frequency) argument. The presence of the energy dependence (or the
two time arguments) distinguishes the Green's function approach from the Wigner
function scheme described above. Because the Wigner function measures the state of
the device at a particular time, and its evolution is described by a first-order
differential equation, it can only comprehend external interactions which occur
instantaneously in time. Such behavior is termed ``Markovian.'' The energy dependence
of the Green's functions permits a description of processes which are not
local in time, or ``non-Markovian'' processes, because the energy argument provides
a way to include convolution integrals over the past history of the system.
An example of a process which is
non-Markovian is the resonant absorption or emission of a phonon. In order for the
energy of the phonon to be well-defined, the interaction must occur over a time
greater than the oscillation period of the phonon. A non-Markovian
Green's function approach can
accurately describe such processes, the Markovian Wigner function approach cannot.
It is fair to say that work on the Green's function approach has produced a great
many mathematical formulations and very few explicit calculations of realistic systems.
Among the latter is the work of Lake and Datta [66].
They model the resonant-tunneling
diode, and include interactions between the electrons and localized phonons. The
locality of the interaction removes the momentum argument from the Green's function,
and also removes any notion of momentum conservation from the model.
One can identify a general principle here, to the effect that if any of the position,
momentum, or energy arguments are missing from the distribution function in a given
theory, then a corresponding conservation law is not enforced within that theory.
If the position argument is not present, as in the case of the Pauli master equation,
then the continuity equation is not enforced. If the momentum argument is absent, as
in the approach of Lake and Datta, then conservation of momentum is not enforced. And
finally, if the energy argument is absent, as in the Markovian Wigner function theory,
then conservation of energy is not enforced. Thus it appears that the only completely
satisfactory theory will be a complete Green's function theory which includes all four
arguments. Such an approach has not yet been developed into a numerically tractable
form.




Next: Summary
Up: Irreversible Processes and
Previous: The Wigner Distribution
William R. Frensley
Fri Jun 23 15:00:21 CDT 1995
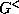 gives the distribution of electrons
(and reduces to the density matrix or Wigner function in certain limits),
gives the distribution of electrons
(and reduces to the density matrix or Wigner function in certain limits), 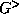 gives
the distribution of holes,
gives
the distribution of holes, 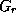 describes time evolution into the future and
describes time evolution into the future and 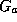 describes time evolution into the past. These Green's functions are determined by
solving a set of Dyson equations (an integral form of Schrödinger 's equation) which
form a convenient starting point for the development of a perturbation expansion.
describes time evolution into the past. These Green's functions are determined by
solving a set of Dyson equations (an integral form of Schrödinger 's equation) which
form a convenient starting point for the development of a perturbation expansion.