A general feature of electron devices is that they are of use only when connected to a circuit, and to be so connected any device must possess at least two terminals, contacts, or leads. As a consequence, every device is a open system with respect to electron flow [5]. This is the overriding fact that determines which theoretical models and techniques may be appropriately applied to the study of quantum devices. For example, the quantum mechanics of pure, normalizable states, such as those employed in atomic physics, does not contribute significantly to an understanding of devices, because such states describe closed systems. To understand devices, one must consider the unnormalizable scattering states, and/or describe the state of the device in terms of statistically mixed states, which casts the problem in terms of quantum kinetic theory.
As a practical matter, a device is of use only when its state is driven far from thermodynamic equilibrium by the action of the external circuit. The nonequilibrium state is characterized by the conduction of significant current through the device and/or the appearance of a nonnegligible voltage drop across the device.
In classical transport theory, the openness of the device is addressed by the definition of appropriate boundary conditions for the differential (or integro-differential) transport equations. Such boundary conditions are formulated so as to approximate the behavior of the physical contacts to the device, typically Ohmic or Schottky contacts [6]. In the traditional treatments of quantum transport theories, the role of boundary conditions is often taken for granted, as the models are constructed upon an unbounded spatial domain. The proper formulation and interpretation of the boundary conditions remains an issue, however, and will be examined in the present work.
It should be understood that, unless otherwise specified, all models to be considered here are based upon a single-band, effective-mass Schrödinger equation. To perform calculations using any of the theories to be discussed and obtain results which may be compared to experimental data, one must numerically evaluate a number of quantities involving fundamental constants. When working with quantum-scale devices, it is convenient to work in a set of metric units chosen to approximate the scale of the phenomena under consideration. Such a set of units is specified in Table 1, and the frequently-used physical constants are given in Table 1 in terms of these units.
Table 1: Convenient Units for Quantum Transport Calculations
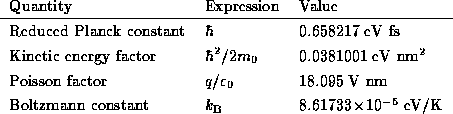
Table 2: Values of Frequently Used Constants