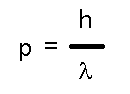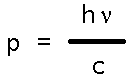Lecture Notes from CHM 6484
3 September 1996
Einstein's Conservation Law
Thermodynamics always begins with weighty laws handed down from previous generations with the solemnity and reverence due all Ancient Wisdom. We will get to them too in good time and, one hopes with reverence, since like the Code of Hammurabai in Jurisprudence, the thermodynamic laws codify understanding and clarify application. Indeed, I've chosen to begin this course somewhat irreverently by toying with the weighty conservation laws in an interdisciplinary way in the hopes of generating connections interesting enough to entice students to follow their least loved aspects of Chemistry.
As chemists, we take conservation laws for granted. Our very stoichiometry depends upon conservation of mass (indeed atoms!), and our thermal and spectral toys are predicated upon the conservation of energy in its many forms. But that image above is a niggling reminder that Einstein would have us conserve matter+energy instead of either alone. The picture is of the Comanche Peak Nuclear Power Reactor near Glen Rose, Texas, southwest of Fort Worth. [Click on it and your browser will get you an enlargement, but don't forget to click your "BACK" button to return here to the notes.]
In the reactor, unstable nuclei radiodecay into their fission products the mass of which falls short of the starting nucleus. We're not disturbed that mass isn't conserved; indeed, TU Electric (the donor of the image) is ecstatic with the failure of mass conservation since they make a profit off the resulting failure of energy conservation! And we're comfortable since we recall that Einstein found the conversion factor between mass and energy, namely, the square of the speed of light!
Surely the world's most recognized scientific equation isn't Newton's F=ma but rather Einstein's
E=moc2.
E=moc2, however, wasn't satisfactory since it only accommodated matter at rest (that's the meaning of the subscript "o"). If matter is in motion, it has the property of motion called momentum, p=mv (mass times velocity), which, in the absence of forces, is itself a conserved quantity.
More to the point, one important component of the energy Einstein needs to conserve is kinetic energy given by the expression,
K = ½ mv2 = p2/2m.
So the expression Einstein actually used for this matter/energy conservation equation was one incorporating momentum appropriately. And it turned out to be something a bit more complex:
E = [ mo2c4 + p2c2 ] ½
Clearly, when p=0, we recover what we expect, but, when it's not, the rest may look foreign to chemists. It isn't. They may not know that they know it yet, but it draws together things chemists take for granted in an interesting way.
Good pedagogy would demand that I have explained before now that Einstein's here in my lecture because his seminal work permeates and informs Chemistry. We chemists recognize that Chemistry wouldn't be save for the properties of electrons! The bonding glue of G.N. Lewis, electrons create our molecules by encouraging atoms to hang together. They create molecular architecture by obedience to W. Pauli and his principle that no more than two electrons share an atomic/molecular orbital. (How would you make DNA with only s electrons, eh?)
And electrons can pull off that stunt only because they are intensely relativistic, a la Einstein. Let me explain. You remember Einstein's other most famous pronouncement: "Nothing can go faster than light?" We'll need a quantitative expression for that soon, so let's introduce it here:
m = mo / [ 1 - (v/c)2 ] ½
As velocity approaches c, the speed of light, mass becomes, well, more massive...indefinitely. Since heavier things require more force to accelerate, the approach to infinite mass as v nears c means no finite force can permit matter to break the Light Speed Barrier!
We chemists are confident that our chemical energies never approach those for which that mass dilation would be a problem, but we're wrong. Remember the reason we aren't struck by the moon (except in bad romances) is because its angular momentum about us could not be conserved if its distance to us collapsed to zero. The same centripetal principle prevents p, d, f, etc. electrons from falling into the nucleus. But s electrons (zero angular momentum) have no such fail safe; indeed, their wavefunctions actually explore the nucleus since they've no node there. What's the problem?
The problem is that potential energy attraction between the electron and proton is indefinitely large at infinitesimal distances. That means the electron could go as fast as it pleases, rushing toward the nucleus. Not so, says Einstein. Thus P.A.M. Dirac takes the trouble to rederive the Schrödinger Equation relativistically to see why not. And lo, the s electron isn't entirely angular momentum free! Dirac's equations show a residual "spin" sufficient to make the s electron miss the nucleus and save the Speed of Light for...well...Light.
And that spin ½ makes all electrons Fermions, that is, critters which obey Pauli's Principle. Hence Relativity is as central to chemistry as is Quantum Mechanics.
Indeed, as chemists, our second favorite particle after the electron would have to be the photon. (We'll not be concerned that, with spin 1, she's a Boson at least for a little while yet.)
And Einstein derived
E = [ mo2c4 + p2c2 ] ½
to satisfy not just matter (like electrons) but also light (photons). While light has no rest mass, it does have momentum, p, and that momentum bears the same relation to light's wavelength that deBroglie claimed obtained for matter! In fact, that's an easy way of remembering the relationship:
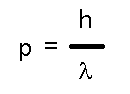
which works for both mass and light. But we also know that light has a frequency as well as a wavelength and that the two are related (as for any wave) to the speed (of light, c).
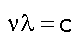 which is really nothing more obscure than d/t=v, the standard expression for speed (except that the frequency needs to be viewed in its "cycles PER second" aspect as the inverse of the oscillation period "SECONDS per cycle" to make it obvious that it's 1/t).
which is really nothing more obscure than d/t=v, the standard expression for speed (except that the frequency needs to be viewed in its "cycles PER second" aspect as the inverse of the oscillation period "SECONDS per cycle" to make it obvious that it's 1/t).
Substituting into deBroglie's relation gives us the expression Einstein would've written down instinctively as the momentum of light, viz.,
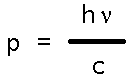
Which makes pc the politically correct expression for the energy of light given by Max Planck!
So for a zero rest mass photon, E = pc, or Planck's constant times frequency, just as we knew it must! But this great conservation expression, E = [ mo2c4 + p2c2 ] ½, holds one more amusing surprise for us chemists. We see it work as expected for both light and resting masses, but what happens when mass is in (non-relativistic) motion? Can we recover what we know must be true about kinetic energy, for example?
Sort of.
That momentum, p, incorporates mass, m, and must therefore be subject to dilation near lightspeed. If we substitute p = mv and the mass dilation law into the above, we get:
E = { mo2c4 + mo2v2c2 / [1 - (v/c)2] } ½
We can easily factor out the rest mass and a c squared. The rest rearranges algebraically to yield:
E = moc2 / [1 - (v/c)2] ½
And only now do we concede that our speeds of interest are tiny, v <<< c. That makes v/c so small that we can expand the denominator in its (square of) v/c series, keeping only the lead terms. (If v/c squared is trivial, higher powers of v/c will be meaninglessly tiny. Ignore 'em.)
E = moc2 [1 + ½ (v/c)2] = moc2 + ½ mov2
And with great relief we recognize kinetic energy emerge in the limit where mass dilation doesn't.
How long does the relief last after we notice that potential energy has not emerged? Einstein didn't leave it out; it's there...hidden...inside the rest mass!
Just as the massive potential energies of the nucleus when rearranged in a radiodecay make significant inroads on the conservation of matter (in its tradeoff with nuclear energy release), so too do even the gentler potentials of electrostatic attraction (of electron to proton, say) extract their attogram of flesh. But that's just it; chemical potentials are so trivial compared to nuclear that rest mass loss is completely invisible. So we chemists are entirely entitled to cling to conservation of mass as long as we invent potential energies to trade off against kinetic in meaningful ways!
These potentials are no less real for this construction. The mass deficits in (non-radio-) chemistry have no impact on our expressions of kinetic energy beyond those modelled by the concepts of potential energy. Trust me: Einstein wouldn't have given up potential energy as a tool for a second!
Return to the CHM 5414 Lecture Notes or Go To Next Lecture.
Chris Parr
University of Texas at Dallas
Programs in Chemistry, Room BE3.506
P.O. Box 830688 M/S BE2.6 (for snailmail)
Richardson, TX 75083-0688
Voice: (972) 883-2485
Fax: (972) 883-2925
BBS: (972) 883-2168 (V.34) or -2932 (V.32bis)
Internet: parr@utdallas.edu (Click on that address to send Dr. Parr e-mail.)
Last modified 17 July 2009.