
Lecture Notes from CHM 6484
5 September 1995
Ideal Gas Thermometer
Those balloons are a sort of Ideal Gas thermometer. They rise and fall on density differences resulting from temperature differences between the air in the bag and that outside. Given the weights and volumes of the balloon and the temperature within the bag, one can deduce the atmospheric temperature outside the bag. We discuss below the fundamental expression, PV=nRT, which permits this.
Chemistry has been called (only half facetiously) the Science of all things whose negative logarithm varies inversely with temperature.
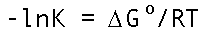 And it's hard to miss examples of this. The course is aiming toward a fundamental understanding of the equilibrium constant expression at left which certainly fits the description. Indeed you can dredge up from memory a wealth of similar examples...Arrhenius rate constants, for example.
And it's hard to miss examples of this. The course is aiming toward a fundamental understanding of the equilibrium constant expression at left which certainly fits the description. Indeed you can dredge up from memory a wealth of similar examples...Arrhenius rate constants, for example.
We'll soon discover TEMPERATURE to be a measure of molecular motion, but since we will have to use it extensively in thermodyamics as an extensive parameter and a mathematical integrating factor, we should pay some heed to how its measure relates to fundamental physical principles.
There are, of course, many physical, chemical, and biological phenomenona which are temperature dependent. Any of these could be used as a crude thermometer. For example, crickets chirp with decreasing rest periods as T rises! We take our own temperature via the thermal expansion of mercury, Hg. But pharmacies sell thermocouple (bimetallic voltage difference) and even liquid crystal (disorientation effects) thermometers for that purpose too.
Very high temperatures are estimated by spectral comparisons to Blackbody Radiation. Very low temperature measurements exploit population differences in eigenstates separated by fractions of wavenumbers.
But all of these are standardized against the classical thermometer which uses the expansion of an Ideal Gas via PV=nRT. If we can derive PV=nRT from more fundamental physical principles, we have a handle on T as PV/nR, and the Ideal Gas Thermometer has some reality. This will require Newton's F=ma (valid macroscopically), asymptotically ideal conditions (approachable experimentally), and U=(1/2)RT, the Equipartition Theorem.
Kinetic theory gives us the first two of these; faith gives us the last. Faith? Is this surreptitious religiosity? In a way, yes. All Science is predicated upon world views (paradigms) which seem useful in explaining the universe. Conservation of Mass is one such, but we've seen last lecture how that had to be extended to encompass radioactivity! Newton's deterministic mechanics had to be supplemented with quantum mechanics for atomic dimensions. These are examples of (exciting) paradigm shifts, but between such shifts, and until they fail, we cling (religiously) to the current paradigm!
(If you want the 1st Year Physics look at Kinetic Theory, sign in as "guest" with password "guest" the University of Illinois Phys 101 Lecture #19.)
In the current paradigm, each mole of (fully available) energy repositories (e.g., translations and rotations) has an average equilibrium thermal energy, U, of (1/2)RT.
Actually, each quadratic term in the energy expression (Hamiltonian) for a mode of motion is so entitled. Vibration, as it turns out, has two such quadratic terms, one (kinetic) involving squared momentum and another (potential) involving squared displacement. So vibrational modes are entitled to twice the average thermal energy of translations, say, for a total of U=RT.
Ideality is a tad easier to believe even though it is only arrived at in a truly tenuous limit. For our purposes, it rests upon two requirements, both achieved as the gas density approaches zero.
First, the volume, V, must all be available to any gas molecule. But we know that each molecule has its own inherent inviolable volume demonstrated by the finite size of the condensed gas. Nevertheless, as the container dimensions increase, the molecular volumes represent a vanishingly small contribution, presumed zero.
 Second, the mean free path of any gas molecule (before collision with another) must be enormous compared to molecular dimensions. If that's not the case, as any given molecule strikes the wall, it's neighbors retard its collision velocity with their attractive long-range forces.
Second, the mean free path of any gas molecule (before collision with another) must be enormous compared to molecular dimensions. If that's not the case, as any given molecule strikes the wall, it's neighbors retard its collision velocity with their attractive long-range forces.
V = 
 2c
2c
Z = N
 2c
2c
L = c/Z = 1/
 2N
2N
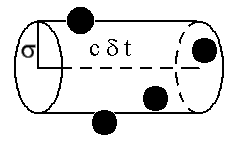
Let that volume, V, above be swept out by a molecule of speed c (no, not the speed of light) as it travels for some small time period. If the intermolecular distance considered collisional is given by sigma (e.g., 4Å for nitrogen). A count of the molecules in the volume (black circles) gives the collision frequency, Z (hits/sec), if the brief period is one second. The count depends on the number density, N, of molecules per unit volume.
Then the mean free path, L, is as given above, and for nitrogen at 1 torr (1/760 atm), L=600Å, comfortably in excess of 4Å! So we are justified in calling nitrogen an ideal gas at 1 torr.
 Finally, we need to calculate the pressure P as a summation of molecular collisional forces, F, on area, A, of the container as P=F/A. Newton assures us that those forces arise by transfer of molecular momentum, p (not P), in elastic collisions with the wall. So we must average these p=mv momenta over all the molecules near the wall (divided by two since half of them, on average, are receding from wall).
Finally, we need to calculate the pressure P as a summation of molecular collisional forces, F, on area, A, of the container as P=F/A. Newton assures us that those forces arise by transfer of molecular momentum, p (not P), in elastic collisions with the wall. So we must average these p=mv momenta over all the molecules near the wall (divided by two since half of them, on average, are receding from wall).
Actually, the collisions aren't elastic; if they were, the gas couldn't pick up thermal energy from a hot wall, right? Instead, given thermal equilibrium of the gas with the wall, the individual inelastic collisions are elastic on average or that equilibrium could not be maintained!
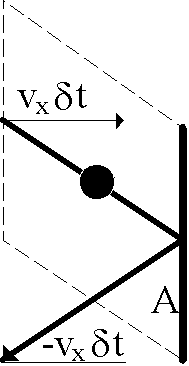
Let the thick vertical line be an area, A, of the wall (seen edge-on, of course). The thick diagonals are the bounce trajectory which, being elastic, leaves the final momentum the same as the initial one but with opposite sign! The molecule has suffered a change in momentum of (negative) twice its original value. Since momentum is conserved (Newton), the wall must've received exactly that magnitude of force (momentum change with time) since F = ma = m(dv/dt) = d(mv)/dt = dp/dt!
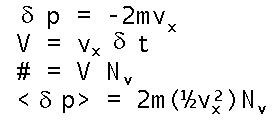 The volume swept by the approaching molecules (per unit area struck) is given by V at left. The number of molecules, #, in that volume is merely the volume times the number density for molecules of speed v. Multiplying the single hit momentum transfer by the number hitting yields the average momentum transferred by collisions with speed v...except that the (previously advertized) factor of 1/2 sneaks in to discriminate between those molecules whose direction is toward the wall (and will thus collide in the next second).
The volume swept by the approaching molecules (per unit area struck) is given by V at left. The number of molecules, #, in that volume is merely the volume times the number density for molecules of speed v. Multiplying the single hit momentum transfer by the number hitting yields the average momentum transferred by collisions with speed v...except that the (previously advertized) factor of 1/2 sneaks in to discriminate between those molecules whose direction is toward the wall (and will thus collide in the next second).
v2 = vx2 + vy2 + vz2
vx2 = vy2 = vz2
(1/3)v2 = vx2
To average over all velocities (which will permit us to use N as the number of all molecules), we note that the average square velocity is the sum of its equal squared components (the Pythagorean theorem)! So any one of the 3 squared components must average to 1/3 of the total.
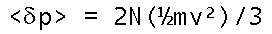 Now we know the average momentum transfer over a unit area of the wall. But since it's already per unit area, this is the pressure! We come in spitting distance of PV=nRT when substitute Avogadro's Number times n/V as the molecular number density.
Now we know the average momentum transfer over a unit area of the wall. But since it's already per unit area, this is the pressure! We come in spitting distance of PV=nRT when substitute Avogadro's Number times n/V as the molecular number density.
P = 2n (½ NAmv2 ) / 3V
P = 2n (½ Mv2) / 3V
½ Mv2 = U = 3 (½RT) or
P = nRT/V
Multiplying the molecular weight, m, by Avogadro's Number to yield the molar weight, M, then gives an expression containing the molar kinetic energy. By the Equipartition Theorem, that must be (3/2)RT since there are 3 degrees of freedom (x, y, and z). The use of the Equipartition Theorem then gives us what we sought, P=nRT/V, or the Ideal Gas equation and the way to measure absolute temperature, T. Of course, we have to agree to keep the gas ideal at low pressures and high temperatures. The latter condition ensures high momentum undeterred by intermolecular attractions.
(Just keep the temperature low enough that the gas doesn't decompose or ionize. Either of those events means extra particles beyond the molecules you intended to have collide with the walls!)
Return to the CHM 5414 Lecture Notes or Go To Next or Previous Lectures.
Chris Parr
University of Texas at Dallas
Programs in Chemistry, Room BE3.506
P.O. Box 830688 M/S BE2.6 (for snailmail)
Richardson, TX 75083-0688
Voice: (972) 883-2485
Fax: (972) 883-2925
BBS: (972) 883-2168 (HST) or -2932 (V.32bis)
Internet: parr@utdallas.edu (Click on that address to send Dr. Parr e-mail.)
Last modified 18 September 1997.

 Second, the mean free path of any gas molecule (before collision with another) must be enormous compared to molecular dimensions. If that's not the case, as any given molecule strikes the wall, it's neighbors retard its collision velocity with their attractive long-range forces.
Second, the mean free path of any gas molecule (before collision with another) must be enormous compared to molecular dimensions. If that's not the case, as any given molecule strikes the wall, it's neighbors retard its collision velocity with their attractive long-range forces. Finally, we need to calculate the pressure P as a summation of molecular collisional forces, F, on area, A, of the container as P=F/A. Newton assures us that those forces arise by transfer of molecular momentum, p (not P), in elastic collisions with the wall. So we must average these p=mv momenta over all the molecules near the wall (divided by two since half of them, on average, are receding from wall).
Finally, we need to calculate the pressure P as a summation of molecular collisional forces, F, on area, A, of the container as P=F/A. Newton assures us that those forces arise by transfer of molecular momentum, p (not P), in elastic collisions with the wall. So we must average these p=mv momenta over all the molecules near the wall (divided by two since half of them, on average, are receding from wall).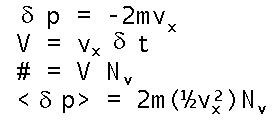 The volume swept by the approaching molecules (per unit area struck) is given by V at left. The number of molecules, #, in that volume is merely the volume times the number density for molecules of speed v. Multiplying the single hit momentum transfer by the number hitting yields the average momentum transferred by collisions with speed v...except that the (previously advertized) factor of 1/2 sneaks in to discriminate between those molecules whose direction is toward the wall (and will thus collide in the next second).
The volume swept by the approaching molecules (per unit area struck) is given by V at left. The number of molecules, #, in that volume is merely the volume times the number density for molecules of speed v. Multiplying the single hit momentum transfer by the number hitting yields the average momentum transferred by collisions with speed v...except that the (previously advertized) factor of 1/2 sneaks in to discriminate between those molecules whose direction is toward the wall (and will thus collide in the next second).