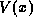 which is constant for
which is constant for 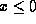 and
and 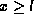 (and which will in
general have different values in these two semi-infinite regions). For
a given energy E such that
(and which will in
general have different values in these two semi-infinite regions). For
a given energy E such that 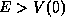 and
and 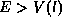 , the general
solution to Schrödinger's equation
, the general
solution to Schrödinger's equation 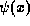 in these regions can be
written as:
in these regions can be
written as:
To sketch the outlines of the QTBM consider a one-dimensional continuum
problem defined by Schrödinger's equation with a potential 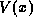 which is constant for
which is constant for 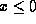 and
and 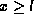 (and which will in
general have different values in these two semi-infinite regions). For
a given energy E such that
(and which will in
general have different values in these two semi-infinite regions). For
a given energy E such that 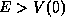 and
and 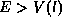 , the general
solution to Schrödinger's equation
, the general
solution to Schrödinger's equation 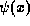 in these regions can be
written as:
in these regions can be
written as:
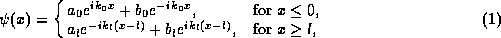
where 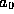 and
and 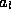 are the amplitudes of the incoming wave
components and
are the amplitudes of the incoming wave
components and 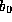 and
and 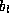 are the amplitudes of the outgoing
wave components. Now, at the left-hand boundary:
are the amplitudes of the outgoing
wave components. Now, at the left-hand boundary:
We may readily solve equation (2) for 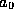 and similarly solve
for
and similarly solve
for 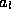 to obtain:
to obtain:
Equations (3) and (4) now provide the QTBM
boundary conditions, if one chooses to specify the values of 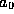 and
and 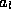 . Boundary conditions of this form are known as Robbins
conditions. They are implicit, in the sense that the values of
. Boundary conditions of this form are known as Robbins
conditions. They are implicit, in the sense that the values of 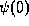 ,
,
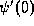 ,
, 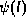 , and
, and 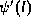 must be obtained by solving
(3) and (4) simultaneously with the
differential equation itself. If one uses a discrete approximation to
Schrödinger's equation
this presents no problem, because the differential equation is reduced
to a set of algebraic equations and the boundary conditions
(3) and (4) simply add two more equations
to this set.
must be obtained by solving
(3) and (4) simultaneously with the
differential equation itself. If one uses a discrete approximation to
Schrödinger's equation
this presents no problem, because the differential equation is reduced
to a set of algebraic equations and the boundary conditions
(3) and (4) simply add two more equations
to this set.