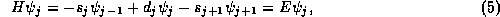
To obtain a useful scheme for numerical evaluation, one must choose a finite basis set on which to express Schrödinger's equation. The traditional approach is to choose a set of orthogonal analytic functions, but for structures with no symmetries specified a priori, such an approach is not optimal. Instead, it is better to expand the Schrödinger equation on a spatially discrete basis. Such schemes may be derived in a number of ways, from a number of conceptual models. For the present purposes, let us consider the derivation simply in terms of a finite-difference approximation to the differential form of Schrödinger's equation. For the effective-mass Schrödinger equation appropriate for semiconductor heterostructures (in which the effective mass may vary with position), the most accurate discretization is[4]
where
and
The equations (5), for all j, form a set of linear
algebraic equations whose matrix representation involves only a
tridiagonal matrix. If one seeks the eigenstates of a bounded system,
the tridiagonal Hamiltonian may be readily diagonalized by standard
numerical techniques. However, we are here concerned with the problem
of the resonances in an unbounded system. This problem must be
formulated in terms of the unbounded scattering states, and to
do this we must
modify the Hamiltonian matrix by incorporating the QTBM boundary
conditions. In the discrete case,
it is simpler to express
the QTBM conditions as a linear combination of the values of  on
two adjacent meshpoints. If the points j = 1 and j = n are the
limits of the domain in which the potential can vary, we may add
boundary points at j = 0 and j = n+1. The form of the wavefunction
will be taken to be:
on
two adjacent meshpoints. If the points j = 1 and j = n are the
limits of the domain in which the potential can vary, we may add
boundary points at j = 0 and j = n+1. The form of the wavefunction
will be taken to be:
where we are writing the propagation factor as z to include both propagating and evanescent states. The values of z at the boundaries are obtained by solving Schrödinger's equation in the boundary neighborhoods:
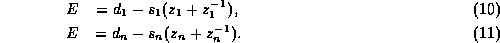
In all cases, if z is a solution, then so is 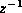 , as a
consequence of time-reversal invariance. When we write z we mean
that solution of the resulting quadratic equation for which
, as a
consequence of time-reversal invariance. When we write z we mean
that solution of the resulting quadratic equation for which 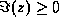 and
and 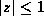 (which describes incoming waves). The wavefunctions
near the boundaries may thus be written:
(which describes incoming waves). The wavefunctions
near the boundaries may thus be written:
To obtain the QTBM equations, one solves (12--15) for
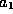 and
and 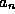 , obtaining
, obtaining
Adding (16--17) to the matrix representation to Schrödinger's equation (5) we obtain the linear system to be solved:
To find the left-incident scattering state one would simply set 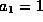 and
and 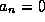 (and conversely for the right-incident state) and
solve the tridiagonal system for all
(and conversely for the right-incident state) and
solve the tridiagonal system for all 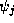 .
.
The matrix in (18) is just the denominator of the
Green's function for Schrödinger's equation, in a space which has been
augmented by adding the incomming traveling wave amplitudes. It
is not, in general, Hermitian, and
consequently admits complex eigenvalues. However, the elements
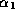 ,
,  ,
, 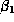 , and
, and 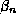 are energy-dependent and thus the eigenvalue problem is nonlinear. The
eigenstates corresponding to those eigenvalues represent ``stationary''
states of Schrödinger's equation with no incident waves. (Of course,
if the energy is complex, the state decays with time, but the decay is
uniformly
exponential at all positions.) These states are just the resonant states
of the system.
are energy-dependent and thus the eigenvalue problem is nonlinear. The
eigenstates corresponding to those eigenvalues represent ``stationary''
states of Schrödinger's equation with no incident waves. (Of course,
if the energy is complex, the state decays with time, but the decay is
uniformly
exponential at all positions.) These states are just the resonant states
of the system.
To evaluate these states we need a method of solving the nonlinear
eigenvalue problem. The technique which has been implemented is to
search for the zeros of the determinant of the matrix 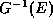 .
To evaluate this determinant we recursively expand
.
To evaluate this determinant we recursively expand  :
:
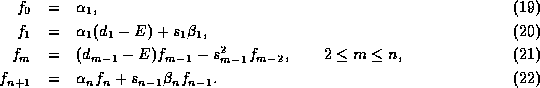
We then solve for E using an algorithm consisting of a linear search to locate the``valleys'' of |f| followed by Newton iteration to find E:

As a result, we obtain 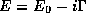 , where the resonance width
, where the resonance width
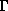 is related to the
escape time by
is related to the
escape time by 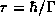 .
.